Предмет: Физика,
автор: alesha667
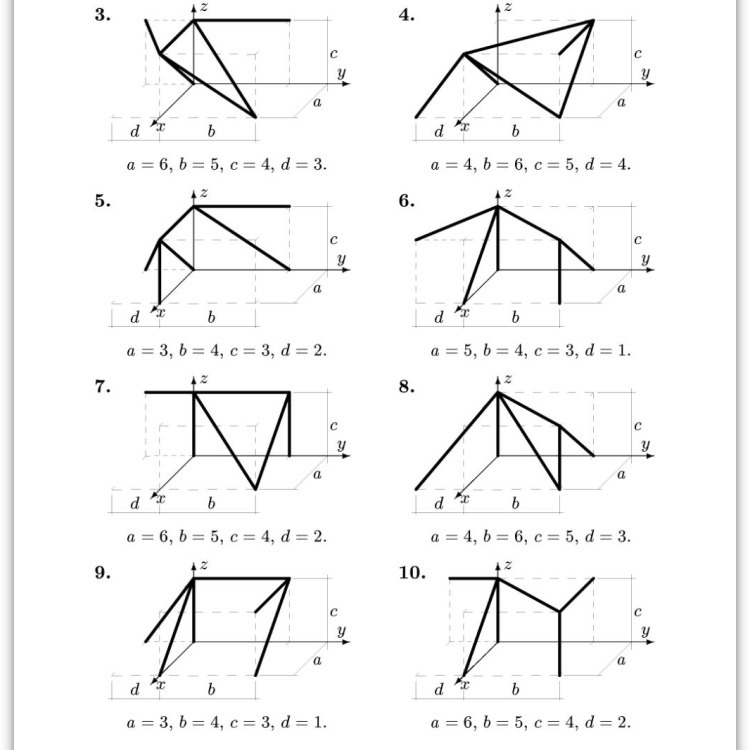
Центр тяжести. Помогите сделать 9 задачу
Приложения:
Ответы
Автор ответа:
1
Координаты Xo, Yo, Zo центра тяжести составной конструкции можно определить через координаты центров тяжести Xoi, Yoi, Zoi и массы Mi частей которые ее составляют. То есть
Xo = сумма(Xoi*Mi)/сумма(Mi)
Yo = сумма(Yoi*Mi)/сумма(Mi)
Zo = сумма(Zoi*Mi)/сумма(Mi)
с суммированием по i = 1 до N, где N - число деталей составляющих сложную конструкцию.
Для стержней равной толщины масса M = p*L, где p - линейная плотность, L - длина, то есть для нашего случая (все стержни конструкции имеют одинаковую линейную плотность) можем от масс перейти к длинам:
Xo = сумма(Xoi*p*Li)/сумма(p*Li) = сумма(Xoi*Li)/сумма(Li)
Yo = .. = сумма(Yoi*Li)/сумма(Li)
Zo = .. = сумма(Zoi*Li)/сумма(Li)
Центр тяжести однородного стержня совпадает с его серединой, то есть
Xoi = (Xi1 + Xi2)/2
Yoi = (Yi1 + Yi2)/2
Zoi = (Zi1 + Zi2)/2
где Xi1, Yi1, Zi1 и Xi2, Yi2, Zi2 - координаты начала и конца i-го стержня
А длина стержня: L = корень((X1 - X2)^2 + (Y1 - Y2)^2 + (Z1 - Z2)^2)
Получаем для X-координаты:
Xo = сумма(Li*(Xoi1 + Xoi2))/(2*сумма(Li))
аналогично для Y и Z.
Всего тут 6 стержней со следующими координатами концов и длиной:
(0, -1, 0) - (0, 0, 3); L1 = корень(0+1+3*3) = 3.16
(3, 0, 0) - (0, 0, 3); L2 = корень(3*3+0+3*3) = 4.24
(0, 0, 0) - (0, 0, 3); L3 = корень(0+0+3*3) = 3.0
(0, 0, 3) - (0, 4, 3); L4 = корень(0+4*4+0) = 4.0
(3, 4, 3) - (0, 4, 3); L5 = корень(3*3+0+0) = 3.0
(3, 4, 0) - (0, 4, 3); L6 = корень(3*3+0+3*3) = 4.24
Сумма длин L = 3.16 + 4.24 + 3.0 + 4.0 + 3.0 + 4.24 = 21.65
Подставляем координаты в формулу, получаем (произведения на ноль опущены):
Xo = (4.24*3+3.0*3+4.24*3)/(2*21.65) = 0.80
Yo = (-3.16*1+4.0*4+3.0*(4+4)+4.24*(4+4))/(2*21.65) = 1.63
Zo = (3.16*3+4.24*3+3.0*3+4.0*(3+3)+3.0*(3+3)+4.24*3)/(2*21.65) = 1.98
Xo = сумма(Xoi*Mi)/сумма(Mi)
Yo = сумма(Yoi*Mi)/сумма(Mi)
Zo = сумма(Zoi*Mi)/сумма(Mi)
с суммированием по i = 1 до N, где N - число деталей составляющих сложную конструкцию.
Для стержней равной толщины масса M = p*L, где p - линейная плотность, L - длина, то есть для нашего случая (все стержни конструкции имеют одинаковую линейную плотность) можем от масс перейти к длинам:
Xo = сумма(Xoi*p*Li)/сумма(p*Li) = сумма(Xoi*Li)/сумма(Li)
Yo = .. = сумма(Yoi*Li)/сумма(Li)
Zo = .. = сумма(Zoi*Li)/сумма(Li)
Центр тяжести однородного стержня совпадает с его серединой, то есть
Xoi = (Xi1 + Xi2)/2
Yoi = (Yi1 + Yi2)/2
Zoi = (Zi1 + Zi2)/2
где Xi1, Yi1, Zi1 и Xi2, Yi2, Zi2 - координаты начала и конца i-го стержня
А длина стержня: L = корень((X1 - X2)^2 + (Y1 - Y2)^2 + (Z1 - Z2)^2)
Получаем для X-координаты:
Xo = сумма(Li*(Xoi1 + Xoi2))/(2*сумма(Li))
аналогично для Y и Z.
Всего тут 6 стержней со следующими координатами концов и длиной:
(0, -1, 0) - (0, 0, 3); L1 = корень(0+1+3*3) = 3.16
(3, 0, 0) - (0, 0, 3); L2 = корень(3*3+0+3*3) = 4.24
(0, 0, 0) - (0, 0, 3); L3 = корень(0+0+3*3) = 3.0
(0, 0, 3) - (0, 4, 3); L4 = корень(0+4*4+0) = 4.0
(3, 4, 3) - (0, 4, 3); L5 = корень(3*3+0+0) = 3.0
(3, 4, 0) - (0, 4, 3); L6 = корень(3*3+0+3*3) = 4.24
Сумма длин L = 3.16 + 4.24 + 3.0 + 4.0 + 3.0 + 4.24 = 21.65
Подставляем координаты в формулу, получаем (произведения на ноль опущены):
Xo = (4.24*3+3.0*3+4.24*3)/(2*21.65) = 0.80
Yo = (-3.16*1+4.0*4+3.0*(4+4)+4.24*(4+4))/(2*21.65) = 1.63
Zo = (3.16*3+4.24*3+3.0*3+4.0*(3+3)+3.0*(3+3)+4.24*3)/(2*21.65) = 1.98
Похожие вопросы
Предмет: Геометрия,
автор: hot67777
Предмет: Геометрия,
автор: gurebugleb228
Предмет: Литература,
автор: zumahandaana030
Предмет: Математика,
автор: lianakosyan76