Предмет: Алгебра,
автор: godboy27
Интегралы............................................
Приложения:
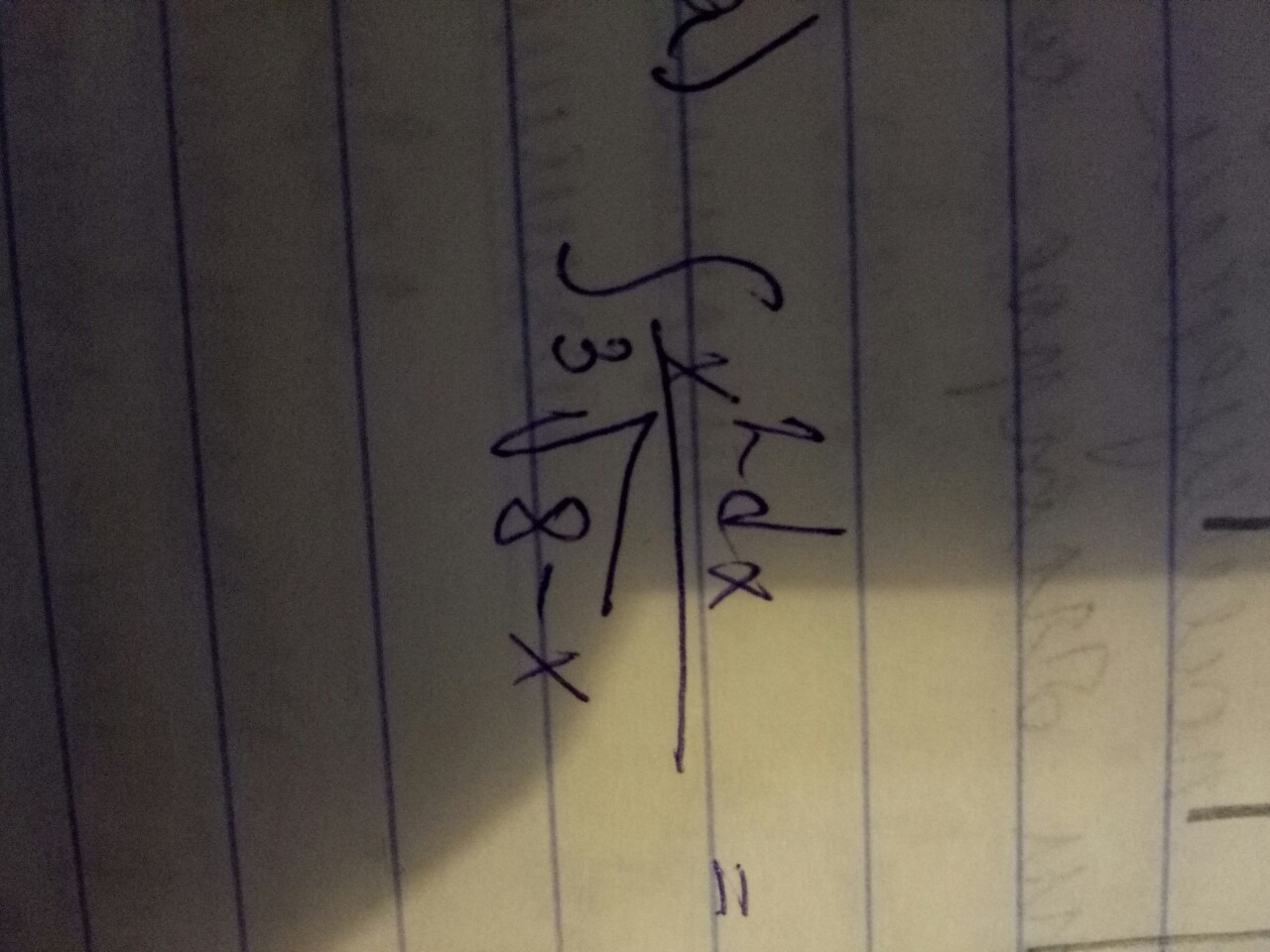
Ответы
Автор ответа:
1
Для того чтоб решить интеграл воспользуемся формулой интегрирования по частям

выполним замену
![\displaystyle U(x)=x^2; dU(x)=2xdx\\\\dV(x)= \frac{1}{ \sqrt[3]{8-x}};\\\\ V=\int (8-x)^{-1/3}dx= (8-x=t;-dx=dt)=\int -t^{1/3} dt= - \frac{3}{2}t^{2/3}=\\\\=- \frac{3}{2}(8-x)^{2/3} \displaystyle U(x)=x^2; dU(x)=2xdx\\\\dV(x)= \frac{1}{ \sqrt[3]{8-x}};\\\\ V=\int (8-x)^{-1/3}dx= (8-x=t;-dx=dt)=\int -t^{1/3} dt= - \frac{3}{2}t^{2/3}=\\\\=- \frac{3}{2}(8-x)^{2/3}](https://tex.z-dn.net/?f=%5Cdisplaystyle+U%28x%29%3Dx%5E2%3B+dU%28x%29%3D2xdx%5C%5C%5C%5CdV%28x%29%3D+%5Cfrac%7B1%7D%7B+%5Csqrt%5B3%5D%7B8-x%7D%7D%3B%5C%5C%5C%5C+V%3D%5Cint+%288-x%29%5E%7B-1%2F3%7Ddx%3D+%288-x%3Dt%3B-dx%3Ddt%29%3D%5Cint+-t%5E%7B1%2F3%7D+dt%3D+-+%5Cfrac%7B3%7D%7B2%7Dt%5E%7B2%2F3%7D%3D%5C%5C%5C%5C%3D-+%5Cfrac%7B3%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D++)
теперь подставляем с формулу
![\displaystyle \int \frac{x^2}{ \sqrt[3]{8-x}}dx=x^2*(- \frac{3}{2}(8-x)^{2/3})- \int - \frac{3}{2}(8-x)^{2/3}*2xdx=\\\\=- \frac{3x^2}{2}(8-x)^{2/3}+3\int x(8-x)^{2/3}dx \displaystyle \int \frac{x^2}{ \sqrt[3]{8-x}}dx=x^2*(- \frac{3}{2}(8-x)^{2/3})- \int - \frac{3}{2}(8-x)^{2/3}*2xdx=\\\\=- \frac{3x^2}{2}(8-x)^{2/3}+3\int x(8-x)^{2/3}dx](https://tex.z-dn.net/?f=%5Cdisplaystyle+%5Cint++%5Cfrac%7Bx%5E2%7D%7B+%5Csqrt%5B3%5D%7B8-x%7D%7Ddx%3Dx%5E2%2A%28-+%5Cfrac%7B3%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D%29-+%5Cint+-+%5Cfrac%7B3%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D%2A2xdx%3D%5C%5C%5C%5C%3D-+%5Cfrac%7B3x%5E2%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D%2B3%5Cint+x%288-x%29%5E%7B2%2F3%7Ddx++++)
теперь с интегралом опять проделаем такую же операция (интегрирование по частям)

продолжим наше решение
![\displaystyle \int \frac{x^2}{ \sqrt[3]{8-x}}dx= \\\\= \frac{3x^2}{2}(8-x)^{2/3}+3 \bigg (- \frac{3}{5}x(8-x)^{5/3}-\int \frac{-3}{5}(8-x)^{5/3}dx \bigg)=\\\\= \frac{3x^2}{2}(8-x)^{2/3}- \frac{9x}{5}(8-x)^{5/3}+ \frac{9}{5}\int(8-x)^{5/3}dx= \displaystyle \int \frac{x^2}{ \sqrt[3]{8-x}}dx= \\\\= \frac{3x^2}{2}(8-x)^{2/3}+3 \bigg (- \frac{3}{5}x(8-x)^{5/3}-\int \frac{-3}{5}(8-x)^{5/3}dx \bigg)=\\\\= \frac{3x^2}{2}(8-x)^{2/3}- \frac{9x}{5}(8-x)^{5/3}+ \frac{9}{5}\int(8-x)^{5/3}dx=](https://tex.z-dn.net/?f=%5Cdisplaystyle+%5Cint++%5Cfrac%7Bx%5E2%7D%7B+%5Csqrt%5B3%5D%7B8-x%7D%7Ddx%3D+%5C%5C%5C%5C%3D+%5Cfrac%7B3x%5E2%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D%2B3+%5Cbigg+%28-+%5Cfrac%7B3%7D%7B5%7Dx%288-x%29%5E%7B5%2F3%7D-%5Cint++%5Cfrac%7B-3%7D%7B5%7D%288-x%29%5E%7B5%2F3%7Ddx+%5Cbigg%29%3D%5C%5C%5C%5C%3D+%5Cfrac%7B3x%5E2%7D%7B2%7D%288-x%29%5E%7B2%2F3%7D-+%5Cfrac%7B9x%7D%7B5%7D%288-x%29%5E%7B5%2F3%7D%2B+%5Cfrac%7B9%7D%7B5%7D%5Cint%288-x%29%5E%7B5%2F3%7Ddx%3D+++++++++)
пользуясь опять заменой 8-x=t; -dx=dt легко вычислить последний интеграл

выполним замену
теперь подставляем с формулу
теперь с интегралом опять проделаем такую же операция (интегрирование по частям)
продолжим наше решение
пользуясь опять заменой 8-x=t; -dx=dt легко вычислить последний интеграл
Похожие вопросы
Предмет: Английский язык,
автор: angelinaskrebtienko
Предмет: Алгебра,
автор: jdkdkdnxkkdkk8383
Предмет: Математика,
автор: cemileaqaeva1990
Предмет: Литература,
автор: Арти123
Предмет: Алгебра,
автор: катерина264