Question

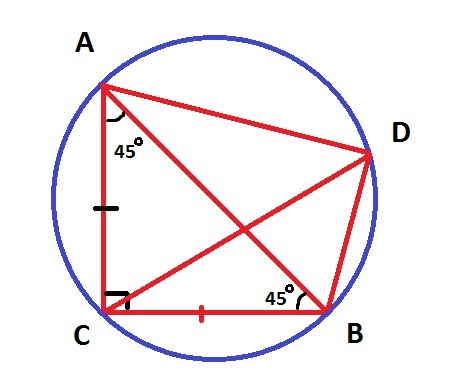
Есть равнобедренный треугольник ABC, угол С=90°. Точка D находится на окружности описывающей АВС, так что получается четырехугольник ADBC. Докажите что АD+DB= (корень из 2)×DC.

Answer 1

По свойству четырехугольника, вписанного в окружность:
"Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон".

То есть: AB*DC= AD*BC+DB*AC

По условию ΔАВС - прямоугольный и равнобедренный, следовательно ∠САВ=∠АВС=45° и АС=ВС, поэтому

AB*DC= AD*BC+DB*ВC

AB*DC= ВС(AD+DB) 

$AD+DB= \frac{AB*DC}{BC} =\frac{AB}{BC}*DC$

Заметим, что в прямоугольном ΔАВС

$\frac{BC}{AB} =sin\angle CAB=sin45^{\circ} = \frac{1}{ \sqrt{2} }$

Тогда: 
$\frac{AB}{BC} = \sqrt{2}$

Следовательно:

AD+DB=√2 DC - ч.т.д.