Предмет: Алгебра,
автор: tuvi
Как мы тут получаем выделенное снизу значение? То что написал внутри квадрата это формула и по формуле не должно быть перед е 1/4 ← как вообше это получаем?
Приложения:
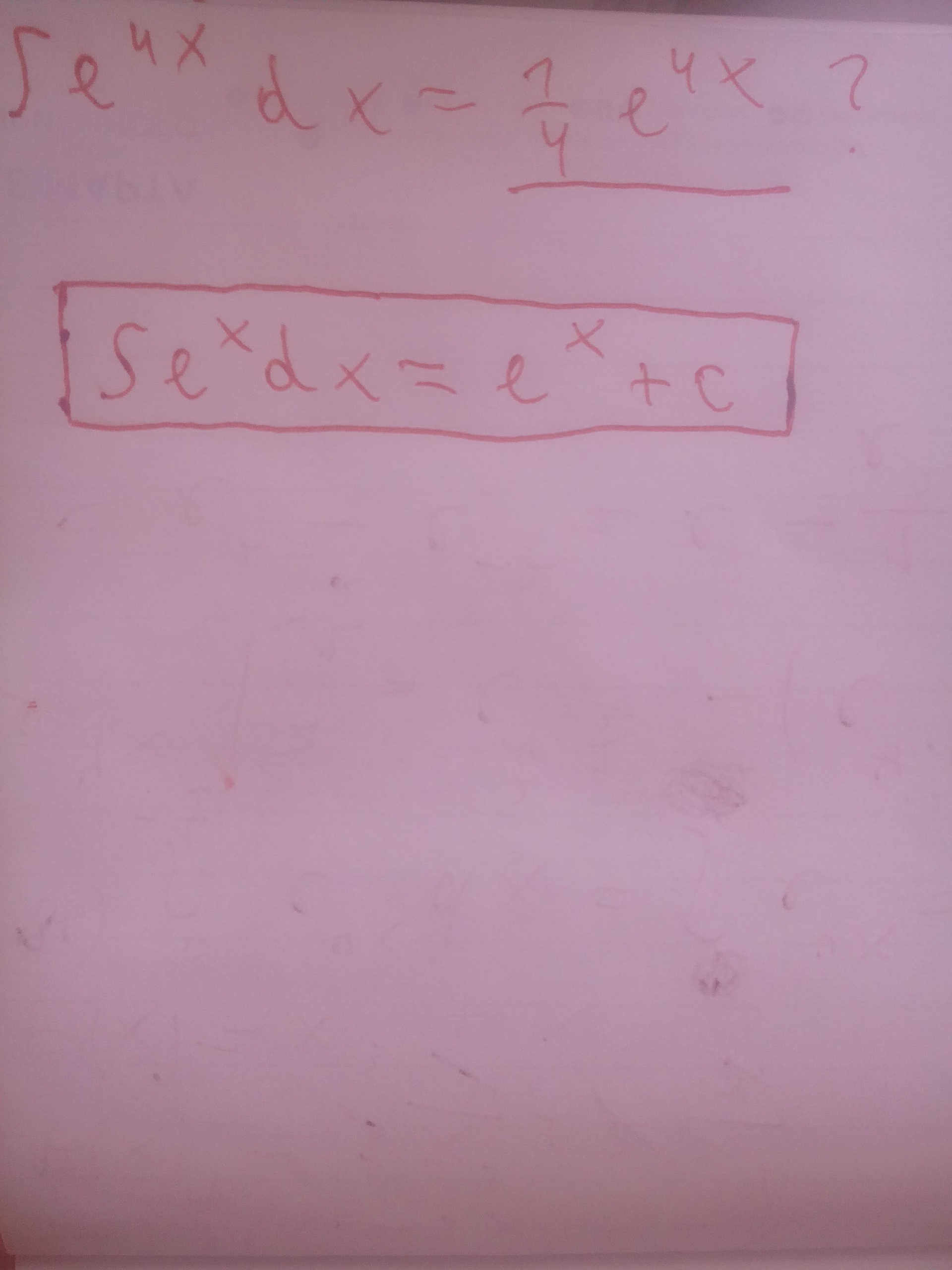
LFP:
в формуле показатель для (е) просто икс... а в задании показатель степени (4х)... замена: 4х = t (4dx = dt) отсюда и 1/4
Погоди сейчас порешаю.
Ничего не дало.
https://znanija.com/task/29299041
Ответы
Автор ответа:
0
∫(e^(4x))dx = (1/4)*∫(e^t)dt = (1/4)* e^t +C = (1/4)* e^(4x) +C
4x = t
4dx = dt
dx = (1/4)dt
4x = t
4dx = dt
dx = (1/4)dt
https://znanija.com/task/29299041
Автор ответа:
0
Функция y =  - сложная, значит, ее производная берется так: y' =
- сложная, значит, ее производная берется так: y' = 
Значит, интеграл будет такой:
Вам же эта четверка не нужна. Поэтому, чтобы от нее избавиться, нужно к первообразной функции добавить
y = *
*  , y' =
, y' =  * 4 *
* 4 *  =
=  - то, что нужно.
- то, что нужно.
Значит,
И Вы забыли добавить константу! Больше не забывайте.
То есть нужно помнить, что Ваша функция - сложная, поэтому нужно избавляться еще и от 4. Просто попробуйте продифференцировать получившуюся функцию обратно - и поймете, что Ваш результат не совпадет с нужным. Надеюсь, что стало чуть-чуть понятнее, если что, готова ответить в комментариях.
Значит, интеграл будет такой:
Вам же эта четверка не нужна. Поэтому, чтобы от нее избавиться, нужно к первообразной функции добавить
y =
Значит,
И Вы забыли добавить константу! Больше не забывайте.
То есть нужно помнить, что Ваша функция - сложная, поэтому нужно избавляться еще и от 4. Просто попробуйте продифференцировать получившуюся функцию обратно - и поймете, что Ваш результат не совпадет с нужным. Надеюсь, что стало чуть-чуть понятнее, если что, готова ответить в комментариях.
ну и константа
Ну а что дальше? Получили исходное выражение.
что конкретно? давайте начнем с производной. e^(4x) - сложная функция, поэтому ее производная - не только e^(4x), но и умножить на (4x)' - отсюда лишняя четверка. но нам нужна только e^(4x), значит, нужно домножить на 1/4, чтобы 4 ушла
у меня не обновлялись комментарии, поэтому не сразу увидела ваш последний
Вверху ещё S было 1/2 а снизу -1/2 это не написал.
в случае с 4e^(4x) по dx проблема в том, что у вас интеграл не тот. я показала, что первообразная e^(4x) не дает тот интеграл, который вам нужен
пределы интегрирования? сейчас не важно, сначала решаем неопределенный интеграл
Я вам сейчас скину ссылку на задание.
https://znanija.com/task/29298694
https://znanija.com/task/29299041
Похожие вопросы
Предмет: Русский язык,
автор: danialmamytov
Предмет: ОБЖ,
автор: majorovasona09
Предмет: Алгебра,
автор: nikitaedik33
Предмет: Химия,
автор: klaczar
Предмет: Математика,
автор: coshkinaanasta