Question

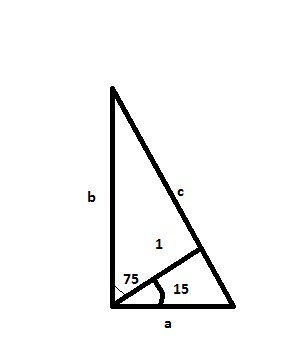
шар вписан в прямую призму, в основании которой лежит прямоугольный треугольник. в этом треугольнике перпендикуляр, опущиный из вершины прямого угла на гипотенузу, равен 1 и составляет с одним из катетов угол 15°. Найдите объем призмы

Answer 1

сos^2(15`)=(1+cos30`)/2=(2+√3)/4; cos15`=√(2+√3)/2
sin^2(15`)=(1-cos30`)/2; sin15`=√(2-√3)/2
a=1/cos15=2/√(2+√3)
b=1/sin15=2/√(2-√3)
c^2=a^2+b^2=16; c=4
r=(a+b-c)/2=√(2-√3)+√(2+√3)-2
H(высота призмы)=2r=2(√(2-√3)+√(2+√3)-2)
S(осн)=сh/2=ab/2=2
V=S(осн)*H=2*2(√(2-√3)+√(2+√3)-2)≈1.8