Предмет: Математика,
автор: 112017
Исследовать на сходимость ряды:
Приложения:
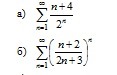
Аноним:
а) признак Даламбера
б) признак Коши
мне нужно решение)
а самим(ой) не вариант? чтото умеете вообще?
для чего этот сайт?
Оба сходятся
можете описать как?
лень...
буду очень благодарна
кое с чем занят.....
Ответы
Автор ответа:
1
а) По признаку Даламбера: 

Ряд сходится.
б) По признаку Коши
![\displaystyle \lim_{n \to \infty} \sqrt[n]{a_n}= \lim_{n \to \infty} \sqrt[n]{\bigg( \frac{n+2}{2n+3}\bigg)^n } = \lim_{n \to \infty} \frac{n+2}{2n+3}= \frac{1}{2}\ \textless \ 1 \displaystyle \lim_{n \to \infty} \sqrt[n]{a_n}= \lim_{n \to \infty} \sqrt[n]{\bigg( \frac{n+2}{2n+3}\bigg)^n } = \lim_{n \to \infty} \frac{n+2}{2n+3}= \frac{1}{2}\ \textless \ 1](https://tex.z-dn.net/?f=%5Cdisplaystyle++%5Clim_%7Bn+%5Cto+%5Cinfty%7D++%5Csqrt%5Bn%5D%7Ba_n%7D%3D+%5Clim_%7Bn+%5Cto+%5Cinfty%7D++%5Csqrt%5Bn%5D%7B%5Cbigg%28+%5Cfrac%7Bn%2B2%7D%7B2n%2B3%7D%5Cbigg%29%5En+%7D+%3D+%5Clim_%7Bn+%5Cto+%5Cinfty%7D++%5Cfrac%7Bn%2B2%7D%7B2n%2B3%7D%3D+%5Cfrac%7B1%7D%7B2%7D%5C+%5Ctextless+%5C+1+++)
Ряд сходится
Ряд сходится.
б) По признаку Коши
Ряд сходится
Похожие вопросы
Предмет: Математика,
автор: pogrebnojboris36
Предмет: Математика,
автор: pomidorkasvezhaya
Предмет: Математика,
автор: Lada54666666655
Предмет: Литература,
автор: Violetta648