Предмет: Математика,
автор: ivanyutenko00
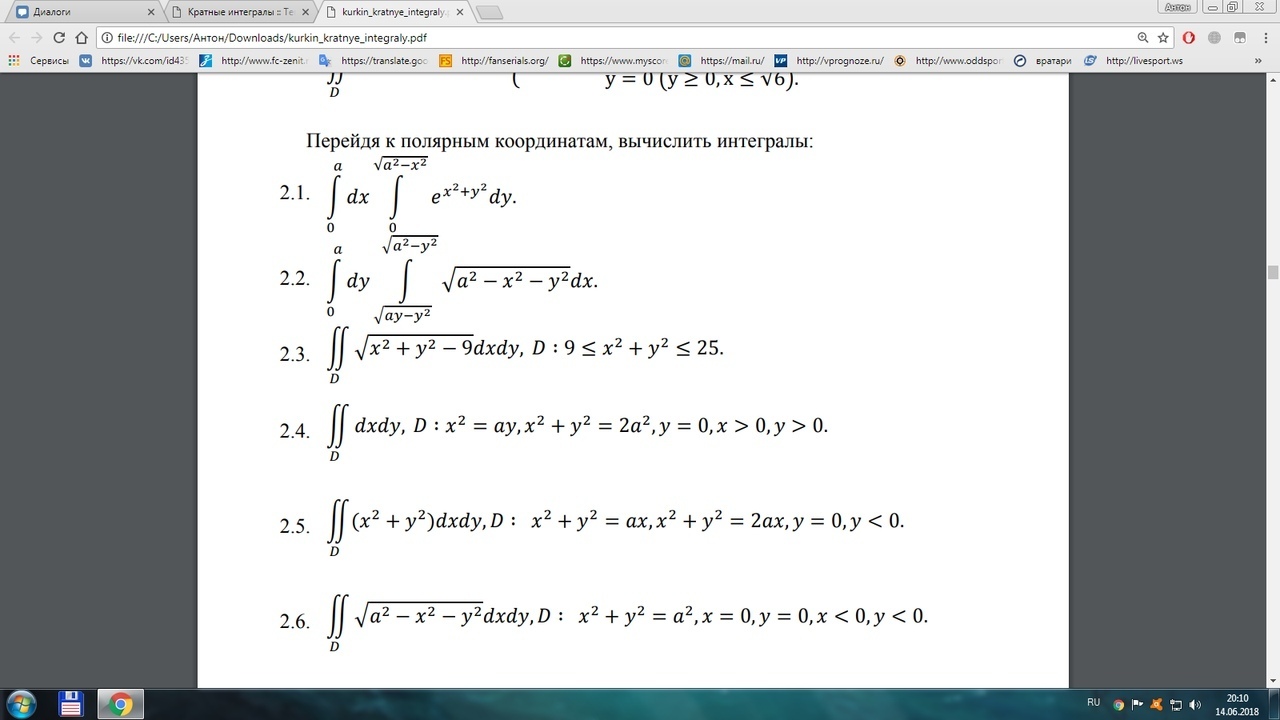
Умоляю,помогите решить. Нужно решить один любой пример из этого задания
Приложения:
Ответы
Автор ответа:
1
ivanyutenko00:
Солнышко,спасибо тебе большое. если бы я в жизни могла бы что-то для тебя сделать,я бы сделала всё. Огромное спасибо) Выручила.
А можешь ещё помочь мне?
Похожие вопросы
Предмет: Физика,
автор: arina77707
Предмет: Литература,
автор: osmontaevzama
Предмет: Математика,
автор: Аноним
Предмет: Экономика,
автор: Аноним
Предмет: Математика,
автор: Златик111