Предмет: Математика,
автор: ivanyutenko00
Помогите решить любой один пример из этого задания.
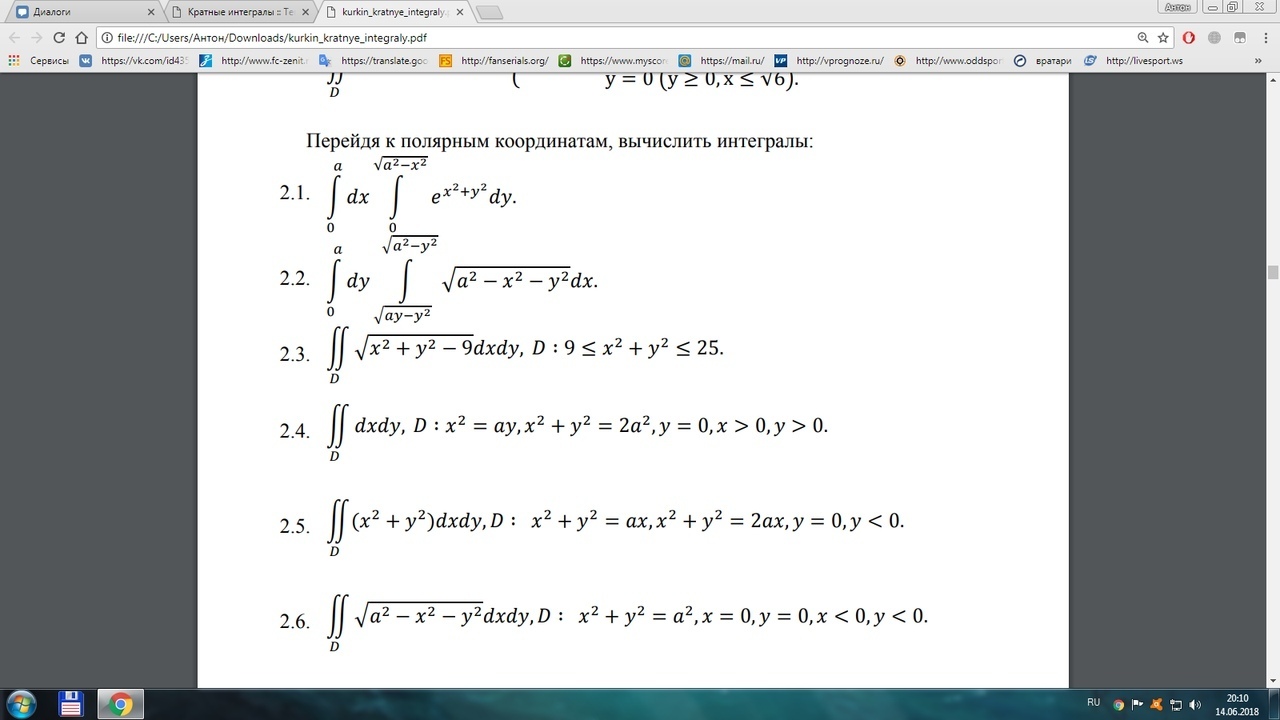
Приложения:
Ответы
Автор ответа:
2
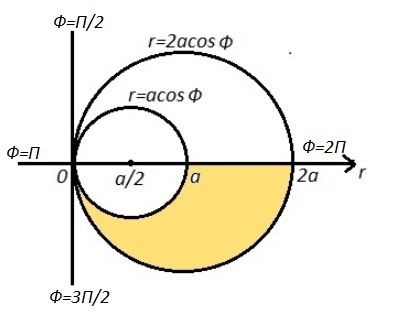
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: kodebardokal
Предмет: Математика,
автор: akyevaaylar510
Предмет: Математика,
автор: UwUxixigdigd
Предмет: Математика,
автор: Златик111
Предмет: Алгебра,
автор: nik1236