Предмет: Геометрия,
автор: Женя123
Угол при вершине осевого сечения конуса равно 90 градусов, а расстояние от центра основания до образующей конуса - 6 см. Найти объем конуса.
Ответы
Автор ответа:
0
Надо найти радиус и высоту
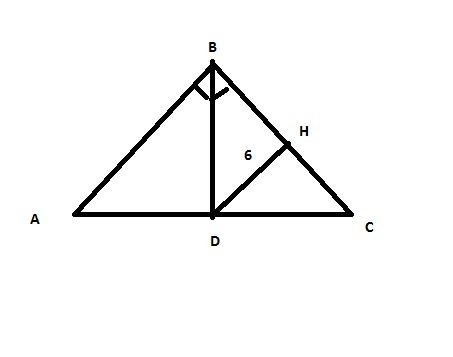
ΔABC-равнобедренный и прямоугольный
<A=<C=45
Такие же ΔDBH и ΔDHC
поэтому BH=HD=HC=6
DC=6√2-это радиус основания
BD^2=BC^2-DC^2=12^2-(6√2)^2=144-72=72
BD=6√2-высота конуса
V=piR^2*h/3=pi*(6√2)^2*6√2/3=pi*144√2
ΔABC-равнобедренный и прямоугольный
<A=<C=45
Такие же ΔDBH и ΔDHC
поэтому BH=HD=HC=6
DC=6√2-это радиус основания
BD^2=BC^2-DC^2=12^2-(6√2)^2=144-72=72
BD=6√2-высота конуса
V=piR^2*h/3=pi*(6√2)^2*6√2/3=pi*144√2
Приложения:
Похожие вопросы
Предмет: Литература,
автор: bogdanstarkov2006
Предмет: Русский язык,
автор: nazmax2008
Предмет: Литература,
автор: euseinov177
Предмет: Математика,
автор: школьник201509
Предмет: Математика,
автор: помогите564