Предмет: Математика,
автор: 1270127
Помогите решить (подробно).
1 пример: сократить дробь
2 пример: упростить вырождение
Приложения:
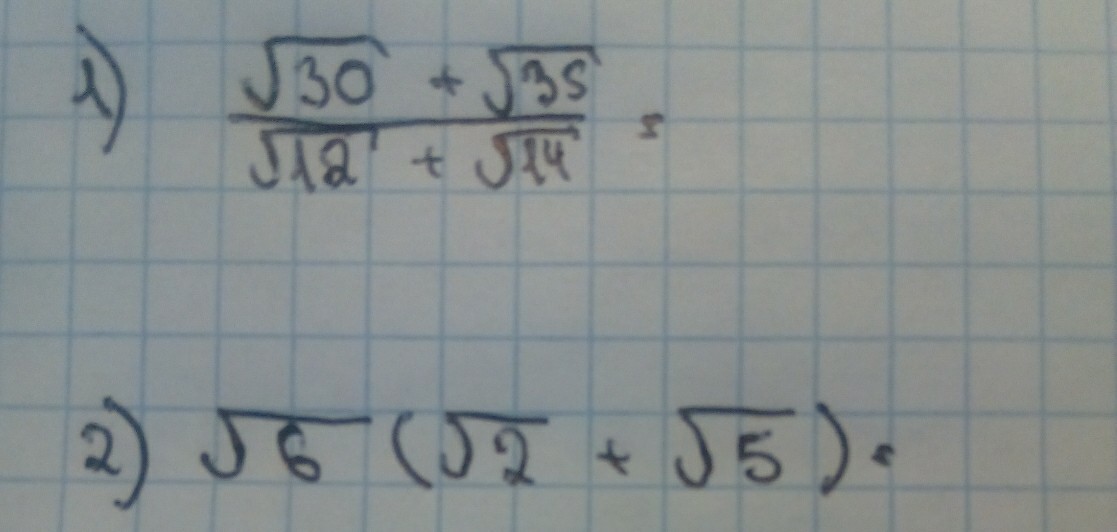
Ответы
Автор ответа:
0
1) tex] \frac{ \sqrt{30}+\sqrt{35} }{\sqrt{12}+\sqrt{14}} =\frac{ \sqrt{5}(\sqrt{6}+\sqrt{7} )}{ \sqrt{2}(\sqrt{6}+\sqrt{7} )}=\sqrt{\frac{5}{2}}
[/tex]
2)
2)
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: sogonov54
Предмет: Биология,
автор: jirgal3232
Предмет: Английский язык,
автор: galya911
Предмет: Математика,
автор: mhousmusic
Предмет: Математика,
автор: zlatakosmacheva