Предмет: Алгебра,
автор: gemasiha
Сначала объясните как вместо dx получаем 1 а потом напишите решение всего задания
Приложения:
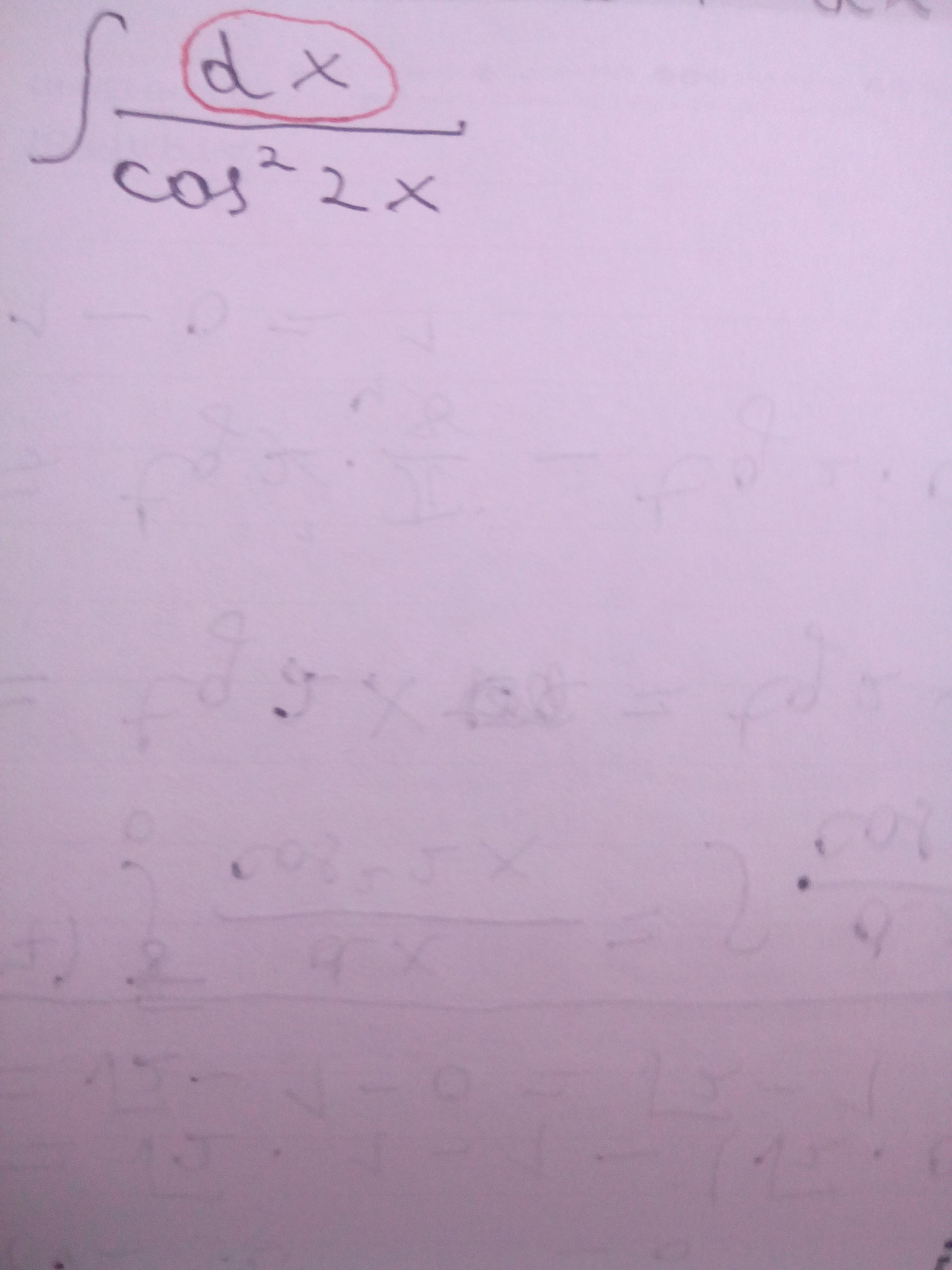
Ответы
Автор ответа:
0
Здесь dx - дифференциал; показывает, что интегрирование идет по переменной x; В общем: 
При этом
Получаем: , C∈R
, C∈R
При этом
Получаем:
Похожие вопросы
Предмет: Алгебра,
автор: krivosheev228007
Предмет: Українська мова,
автор: esuhinin9
Предмет: Алгебра,
автор: Stillg
Предмет: Литература,
автор: avsnlisa