Question

В конусе можно провести три взаимно перпендикулярные образующие. Найдите косинус угла в осевом сечении такого конуса.

Answer 1

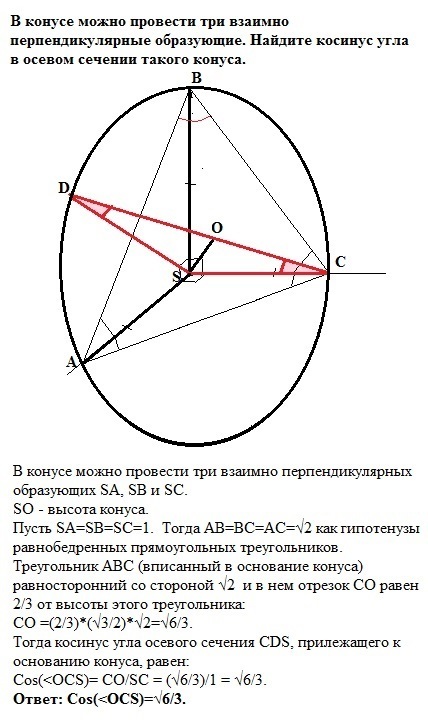
В конусе можно провести три взаимно перпендикулярных образующих SA, SB и SC.
SO - высота конуса.
Пусть SA=SB=SC=1.  Тогда АВ=ВС=АС=√2 как гипотенузы равнобедренных прямоугольных треугольников.
Треугольник АВС (вписанный в основание конуса) равносторонний со
стороной, равной √2  и в нем отрезок СО равен 2/3 от высоты этого треугольника, равной h=(√3/2)*a, где а - сторона треугольника:
CO =(2/3)*(√3/2)*√2=√6/3.
Осевое сечение конуса CDS, проходит через центр основания О.
Тогда косинус угла в осевом сечении, прилежащего к основанию конуса, равен:
Cos(<OCS)= CО/SC = (√6/3)/1 = √6/3.
Ответ: Cos(<OCS)=√6/3 ≈ 0,816.