Предмет: Математика,
автор: aza91
Помогите пожалуйста?
Приложения:
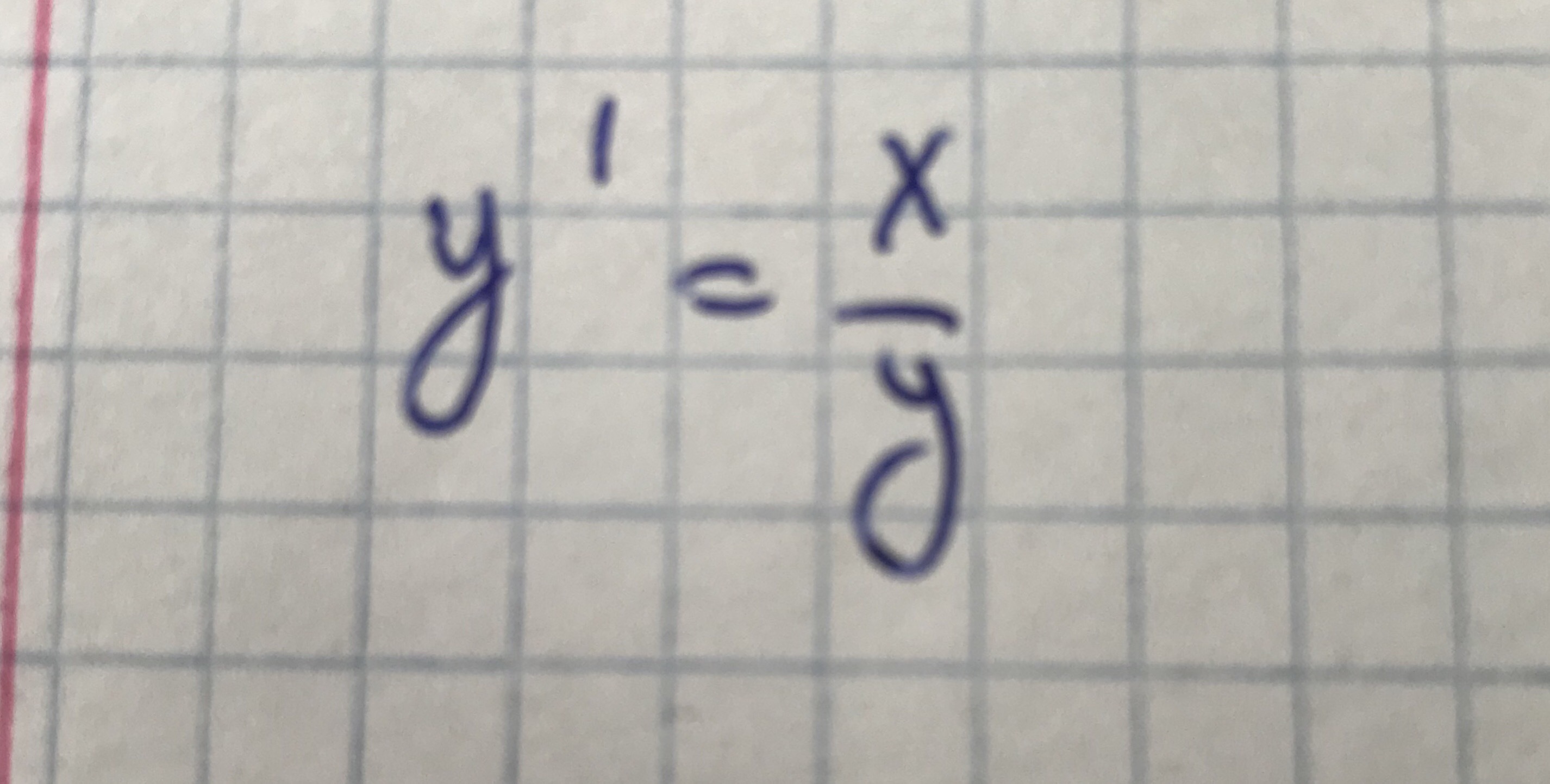
Ответы
Автор ответа:
1
Решение
Интегрируем обе части уравнения
y² = x² + C
y² - x² = C
Получили уравнение гиперболы
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: burdukovskaadasa99
Предмет: Математика,
автор: sofiadorosenko431
Предмет: Информатика,
автор: ruru88
Предмет: Математика,
автор: султан95
Предмет: Математика,
автор: кариша38