Предмет: Геометрия,
автор: Морковка14
Найдите площадь равнобедренного треугольника, если центр вписанной в него окружности делит высоту, проведённую к основанию, в отношении 3:2, считая от вершины, и боковая сторона равна 6.
Приложения:

Ответы
Автор ответа:
1
По условию

AB=6;
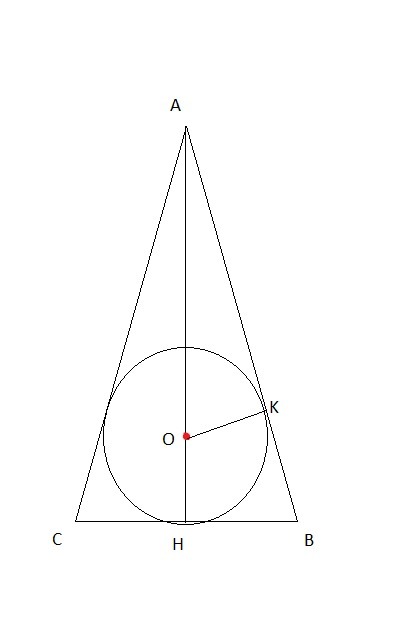
OK - радиус. K - точка касания, поэтому ∠OKA прямой.
Рассмотрим ΔABH и ΔOAK; У них угол OAK общий и они прямоугольные. Следовательно, они подобны. Пусть AO = 3x; OH = 2x; Из подобия имеем: ; OK = OH как радиусы.
; OK = OH как радиусы.
 Откуда
Откуда 
Значит CB = 8; Теперь можем найти площадь S:

AB=6;
OK - радиус. K - точка касания, поэтому ∠OKA прямой.
Рассмотрим ΔABH и ΔOAK; У них угол OAK общий и они прямоугольные. Следовательно, они подобны. Пусть AO = 3x; OH = 2x; Из подобия имеем:
Значит CB = 8; Теперь можем найти площадь S:
Приложения:
Похожие вопросы
Предмет: Физкультура и спорт,
автор: Аноним
Предмет: Математика,
автор: 4elovek4eburek228
Предмет: Математика,
автор: saskeSakuraa
Предмет: Информатика,
автор: Арабат
Предмет: Физика,
автор: jadwor