Question

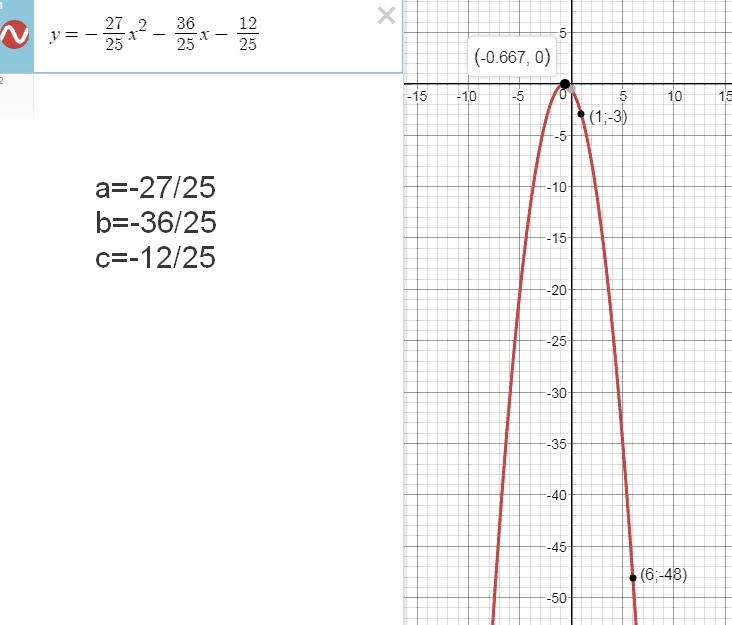
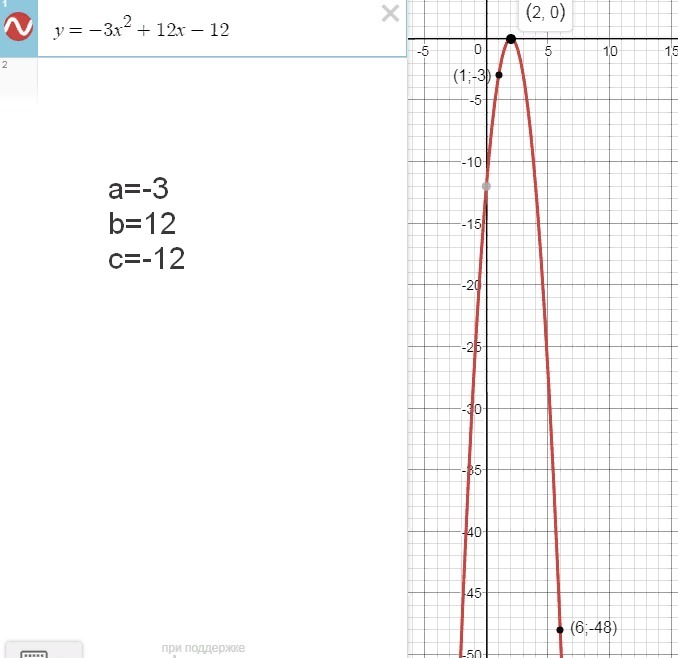
При каких значениях a,b,c график функции y=ax²+bx+c проходит через точки M(1;-3) N(6;-48) и имеет с осью абсцисс одну общую точку.

Answer 1

Парабола имеет с осью абсцисс ровно одну общую точку (в этом случае говорят, что парабола касается оси абсцисс), если дискриминант равен 0

$D=b^2-4ac=0;b^2=4ac;c= \frac{b^2}{4a} \\ \\ \left \{ {{-3=a+b+\frac{b^2}{4a}} \atop {-48=36a+6b+\frac{b^2}{4a}}} \right. \\ \\ 45=-35a-5b \\ 9=-7a-b \\ b=-9-7a \\ \\ -3=a-9-7a+\frac{(-9-7a)^2}{4a} \\ \\ -12a=-36a-24a^2+49a^2+126a+81 \\ \\ 25a^2+102a+81=0 \\ \\ D=10404-4*25*81=10404-8100=2304=48^2$
$a_{1} =(-102-48)/50=-3 \\ b_{1} =-9-7*(-3)=12 \\ c_{1} =144/(-3*4)=-12 \\ \\ y=-3x^2+12x-12 \\ \\ a_{2} =(-102+48)/50=-27/25 \\ b_{2} =-9-7*(-27/25)=-36/25 \\ c_{2} = \frac{(- \frac{36}{25})^2 }{4*(- \frac{27}{25}) } =-12/25 \\ \\ y=- \frac{27}{25} x^2- \frac{36}{25} x- \frac{12}{25}$