Предмет: Алгебра,
автор: ЧёЗаНафиг
ПОМОГИТЕ ПОЖАЛУЙСТА! (СРОЧНО)
Задание: Найти общее решение дифференциальных уравнений
Приложения:
Ответы
Автор ответа:
1
Посмотрите предложенное решение.
Оформление не соблюдалось.
Оформление не соблюдалось.
Приложения:
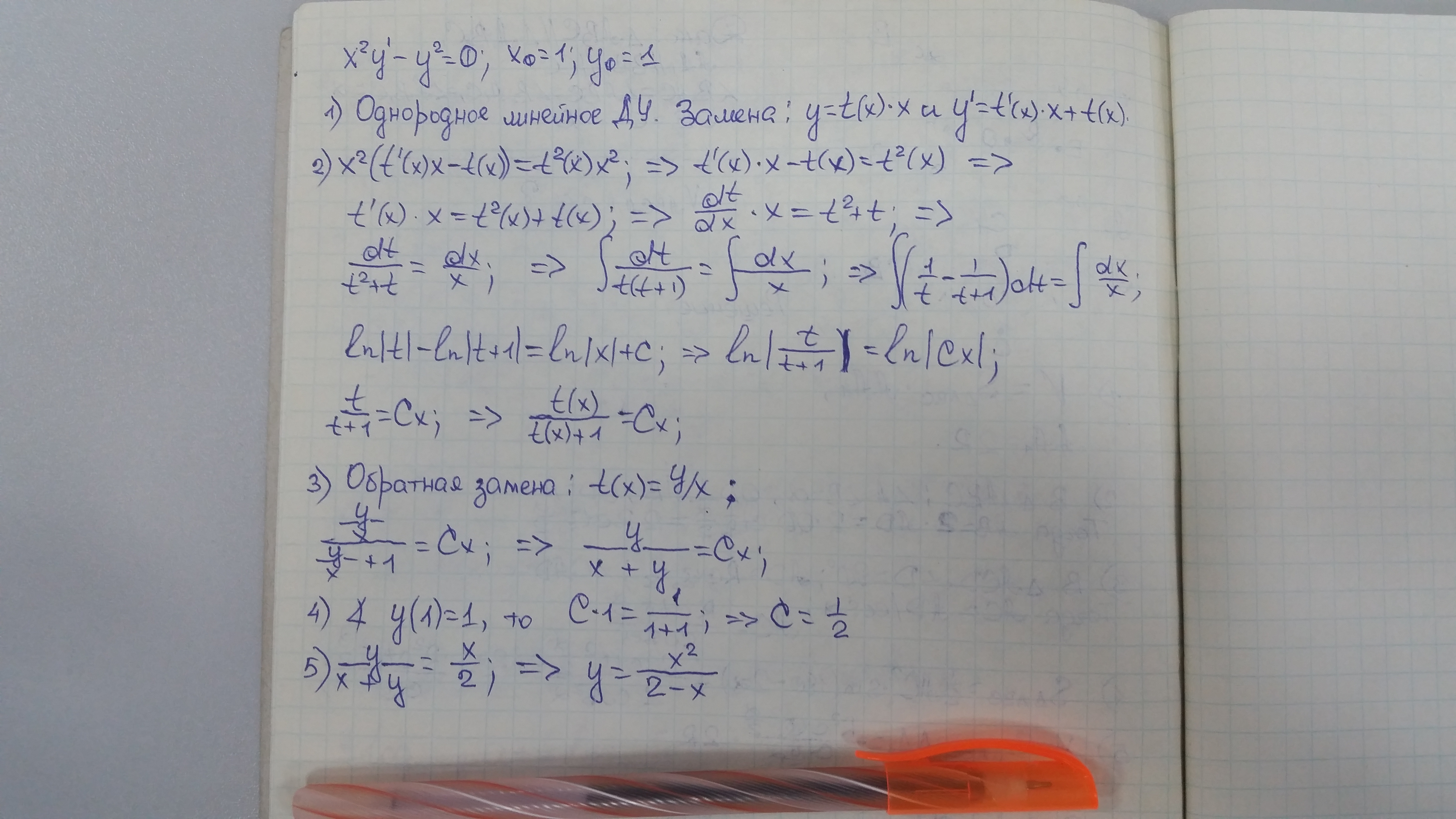
NNNLLL54:
В 3 строчке написали вместо (t'x+t) выражение (t'x-t).
Автор ответа:
1
Уравнение с разделяющимися переменными.

Наверное, лучше бы сразу отметили как неверное. А то вышло, что поставили столько "лайков"...
Просто сразу можно было поправить решение
На работе проекты, никак, решение наскоками... Но в любом случае персональное спасибо.
Похожие вопросы
Предмет: Биология,
автор: gorelykyasja
Предмет: Химия,
автор: inessa2lk
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: argentina2119