Предмет: Математика,
автор: LonelyHunter
Помогите решить пожалуйста. Вычислить интеграл где отрезок L=AB с концами в точках A(1;2), B(2;4).
Приложения:
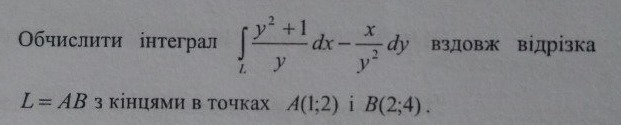
Ответы
Автор ответа:
2
Параметризуем отрезок: (x(t), y(t)) = (t, 2t), где t изменяется от 1 до 2. При этом dx = dt; dy = 2dt.

Похожие вопросы
Предмет: Математика,
автор: ksunyatomilova
Предмет: География,
автор: olenaaa12
Предмет: Алгебра,
автор: kostomarovvitalik153
Предмет: Биология,
автор: dalia5445