Предмет: Математика,
автор: surer211
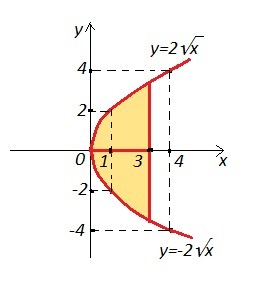
Вычислить площадь поверхности образованной вращением дуги параболы у^2=4х вокруг оси Ох, ограниченной точками О (0;0) и А (3; 2√3).
Ответы
Автор ответа:
2
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mxslwxq
Предмет: Английский язык,
автор: magma19821981
Предмет: Алгебра,
автор: s56712689
Предмет: Математика,
автор: аврора26
Предмет: Литература,
автор: 52511