Предмет: Алгебра,
автор: vepebijuc
Как решить дальше это задание? Напишите все методы решения.
Приложения:
Ответы
Автор ответа:
0
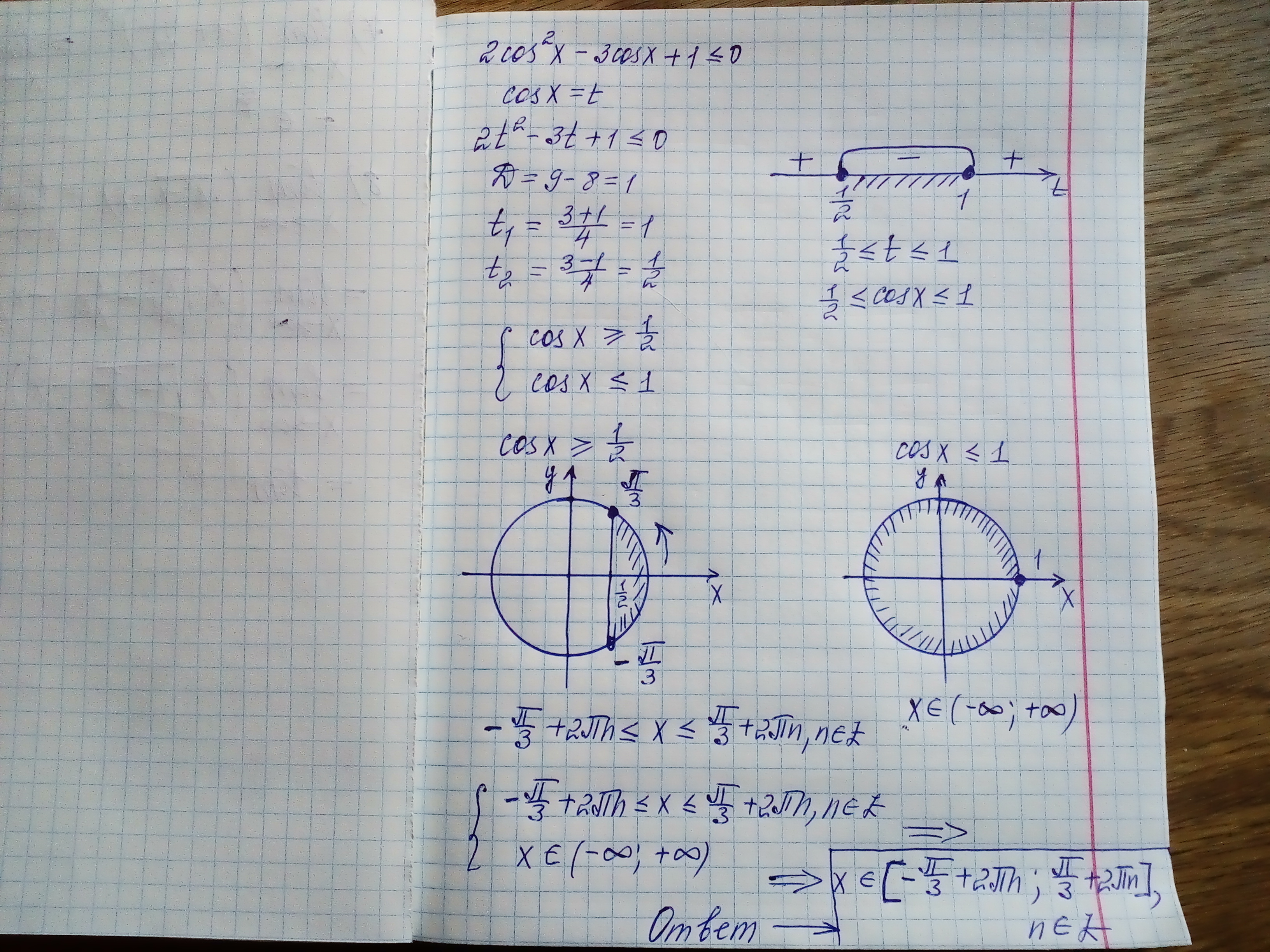
Заданное неравенство является квадратным неравенством относительно функции t=cosx.
![2cos^2x-3cosx+1 \leq 0\\\\t=cosx,\; \; \; -1 \leq t \leq 1\\\\2t^2-3t+1 \leq 0\; ,\; \; t_1=\frac{1}{2}\; \; t_2=1\\\\+++[\, \frac{1}{2}\, ]---[\, 1\, ]+++\; \; \; t\in [\, \frac{1}{2}\; ,\; 1\, ]\; \; \Rightarrow \\\\\frac{1}{2} \leq cosx \leq 1\; \; \; \to \; \; \left \{ {{cosx \geq \frac{1}{2}} \atop {cosx \leq 1}} \right. \; \left \{ {{-\frac{\pi}{3}+2\pi n\leq x\leq \frac{\pi}{3}+2\pi n\; ,\; n\in Z} \atop {x\in (-\infty ,+\infty )}} \right. \; \to \\\\x\in [-\frac{\pi }{3}+2\pi n\; ,\; \frac{\pi }{3}+2\pi n\; ,\; n\in Z](https://tex.z-dn.net/?f=2cos%5E2x-3cosx%2B1+%5Cleq+0%5C%5C%5C%5Ct%3Dcosx%2C%5C%3B+%5C%3B+%5C%3B++-1+%5Cleq+t+%5Cleq+1%5C%5C%5C%5C2t%5E2-3t%2B1+%5Cleq+0%5C%3B+%2C%5C%3B+%5C%3B+t_1%3D%5Cfrac%7B1%7D%7B2%7D%5C%3B+%5C%3B+t_2%3D1%5C%5C%5C%5C%2B%2B%2B%5B%5C%2C+%5Cfrac%7B1%7D%7B2%7D%5C%2C+%5D---%5B%5C%2C+1%5C%2C+%5D%2B%2B%2B%5C%3B+%5C%3B+%5C%3B+t%5Cin+%5B%5C%2C+%5Cfrac%7B1%7D%7B2%7D%5C%3B+%2C%5C%3B+1%5C%2C+%5D%5C%3B+%5C%3B+%5CRightarrow+%5C%5C%5C%5C%5Cfrac%7B1%7D%7B2%7D+%5Cleq+cosx+%5Cleq+1%5C%3B+%5C%3B+%5C%3B+%5Cto+%5C%3B+%5C%3B++%5Cleft+%5C%7B+%7B%7Bcosx+%5Cgeq+%5Cfrac%7B1%7D%7B2%7D%7D+%5Catop+%7Bcosx+%5Cleq+1%7D%7D+%5Cright.+%5C%3B++%5Cleft+%5C%7B+%7B%7B-%5Cfrac%7B%5Cpi%7D%7B3%7D%2B2%5Cpi+n%5Cleq+x%5Cleq+%5Cfrac%7B%5Cpi%7D%7B3%7D%2B2%5Cpi+n%5C%3B+%2C%5C%3B+n%5Cin+Z%7D+%5Catop+%7Bx%5Cin+%28-%5Cinfty+%2C%2B%5Cinfty+%29%7D%7D+%5Cright.+%5C%3B+%5Cto+%5C%5C%5C%5Cx%5Cin+%5B-%5Cfrac%7B%5Cpi+%7D%7B3%7D%2B2%5Cpi+n%5C%3B+%2C%5C%3B+%5Cfrac%7B%5Cpi+%7D%7B3%7D%2B2%5Cpi+n%5C%3B+%2C%5C%3B+n%5Cin+Z "2cos^2x-3cosx+1 \leq 0\\\\t=cosx,\; \; \; -1 \leq t \leq 1\\\\2t^2-3t+1 \leq 0\; ,\; \; t_1=\frac{1}{2}\; \; t_2=1\\\\+++[\, \frac{1}{2}\, ]---[\, 1\, ]+++\; \; \; t\in [\, \frac{1}{2}\; ,\; 1\, ]\; \; \Rightarrow \\\\\frac{1}{2} \leq cosx \leq 1\; \; \; \to \; \; \left \{ {{cosx \geq \frac{1}{2}} \atop {cosx \leq 1}} \right. \; \left \{ {{-\frac{\pi}{3}+2\pi n\leq x\leq \frac{\pi}{3}+2\pi n\; ,\; n\in Z} \atop {x\in (-\infty ,+\infty )}} \right. \; \to \\\\x\in [-\frac{\pi }{3}+2\pi n\; ,\; \frac{\pi }{3}+2\pi n\; ,\; n\in Z")
Приложения:
vepebijuc:
Твой ответ не понятный.
Неравенство относительно t решается с помощью метода интервалов. Затем вместо t подставляешь cosx. Двойное неравенство эквивалентно системе двух неравенств. Далее решается каждое неравенство и в ответ записывается пересечение множеств... Если всё это учить в школе, то всё понятно.
Автор ответа:
0
!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
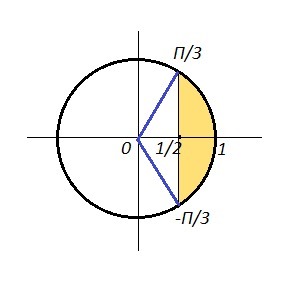
Почти ничего не понятно.
Вот система откуда тут появляется?
Из двойного неравенства ½≤cosx≤1
А это зачем?
Похожие вопросы
Предмет: Биология,
автор: ozpapaougouqvlyqc
Предмет: Алгебра,
автор: lizayevdoshchek
Предмет: Математика,
автор: evgeniaavankina
Предмет: Математика,
автор: Аноним