Предмет: Геометрия,
автор: Infinity167
в правильной четырехугольной усечённой пирамиде стороны основания равны 10 и 22, а диагональ равна 24. найдите площадь боковой поверхности этой пирамиды
Infinity167:
куба
ой
нет
усесенной пирасиды
для внутренней
я его просто переписала
Постоянно появляются задачи "для диагонали куба" или ещё чего то там. В качестве просто диагонали подразумевается пространственная диагональ. А диагонали граней особо выделяются.
Ответы
Автор ответа:
2
--- 1 ---
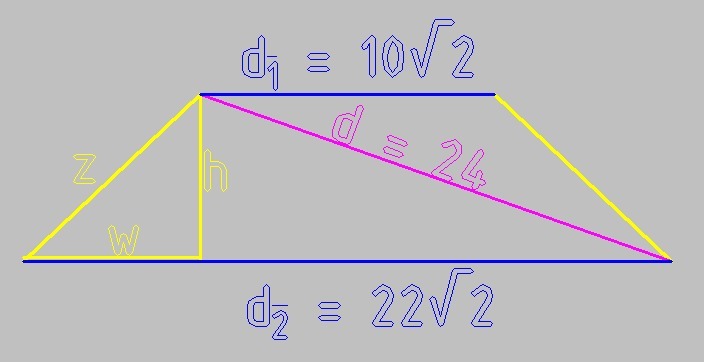
рассмотрим сечение пирамиды в вертикальной плоскости через диагонали верхнего и нижнего оснований
Сечение представляет из себя равностороннюю трапецию, верхнее основание которой по т. Пифагора
d₁ = √(10² + 10²) = 10√2
Нижнее основание
d₂ = √(22² + 22²) = 22√2
Проекция бокового ребра z пирамиды на плоскость основания - w
w = (d₂ - d₁)/2 = (22√2 - 10√2)/2 = 12√2/2 = 6√2
найдём высоту пирамиды h
h² + (d₂ - w)² = d²
h² + (22√2 - 6√2)² = 24²
h² + (16√2)² = 24²
h² + 256*2 = 576
h² = 64
h = 8
И боковое ребро пирамиды
z² = w² + h²
z² = 36*2 + 64 = 72 + 64 = 136
z = √136 = 2√34
--- 2 ---
Теперь рассмотрим боковую грань пирамиды
Это тоже равносторонняя трапеция, её основания 22 и 10, боковые стороны z = 2√34
проекция боковой стороны на основание
(22-10)/2 = 6
высота по Пифагору
√((2√34)² - 6²) = √(136-36) = √100 = 10
Площадь
S = 1/2(10 + 22)*10 = 160
Таких боковых сторон 4
Ответ
S = 4*160 = 640
рассмотрим сечение пирамиды в вертикальной плоскости через диагонали верхнего и нижнего оснований
Сечение представляет из себя равностороннюю трапецию, верхнее основание которой по т. Пифагора
d₁ = √(10² + 10²) = 10√2
Нижнее основание
d₂ = √(22² + 22²) = 22√2
Проекция бокового ребра z пирамиды на плоскость основания - w
w = (d₂ - d₁)/2 = (22√2 - 10√2)/2 = 12√2/2 = 6√2
найдём высоту пирамиды h
h² + (d₂ - w)² = d²
h² + (22√2 - 6√2)² = 24²
h² + (16√2)² = 24²
h² + 256*2 = 576
h² = 64
h = 8
И боковое ребро пирамиды
z² = w² + h²
z² = 36*2 + 64 = 72 + 64 = 136
z = √136 = 2√34
--- 2 ---
Теперь рассмотрим боковую грань пирамиды
Это тоже равносторонняя трапеция, её основания 22 и 10, боковые стороны z = 2√34
проекция боковой стороны на основание
(22-10)/2 = 6
высота по Пифагору
√((2√34)² - 6²) = √(136-36) = √100 = 10
Площадь
S = 1/2(10 + 22)*10 = 160
Таких боковых сторон 4
Ответ
S = 4*160 = 640
Приложения:
у вас ошибка, боковая сторона усечённой пирамиды равна 2√34
поправил
Похожие вопросы
Предмет: Английский язык,
автор: annazema2005
Предмет: Английский язык,
автор: Kirillverbytskyi1105
Предмет: Математика,
автор: Kittylisaa
Предмет: Математика,
автор: avitomain