Предмет: Алгебра,
автор: smile2zz
найти предел
x стремится к -бесконечности sqrt(x^2+4)-sqrt(x^2-3x+1)
Ответы
Автор ответа:
0
Приложения:
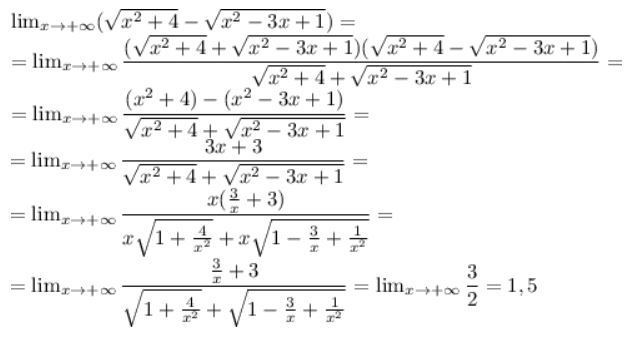
Похожие вопросы
Предмет: Алгебра,
автор: Amogus98751
Предмет: Математика,
автор: nmelnik283
Предмет: Математика,
автор: nazmidinovasafina
Предмет: Математика,
автор: Данила5551