Предмет: Математика,
автор: nedenispolybomy
Решить задачу по теории вероятности. Подробно.
Задание в приложение.
Приложения:
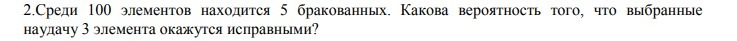
Ответы
Автор ответа:
1
100-5=95 элементов исправных.
Выбрать три исправных элементов можно C(3;95)=95!/3!92!=138415 -ЧИСЛО благоприятных событий
Число все возможных событий: C(3;100)=100!/3!97!=161700
Искомая вероятность: P=138415/161700≈0.86
Выбрать три исправных элементов можно C(3;95)=95!/3!92!=138415 -ЧИСЛО благоприятных событий
Число все возможных событий: C(3;100)=100!/3!97!=161700
Искомая вероятность: P=138415/161700≈0.86
Аноним:
Есть другой способ.
Вероятность того, что один элемент исправный - 95/100, второй 94/99 и третий - 93/98
По теореме умножения Р=(95*94*93)/(100*99*98)
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: География,
автор: vitaha1366
Предмет: Алгебра,
автор: polinaberezina26
Предмет: Геометрия,
автор: vika20031180
Предмет: Литература,
автор: Nyasha07