Предмет: Алгебра,
автор: Maria160000
найдите область определения функции у=корень 3-5х-2х в квадрате \10х-5
Приложения:
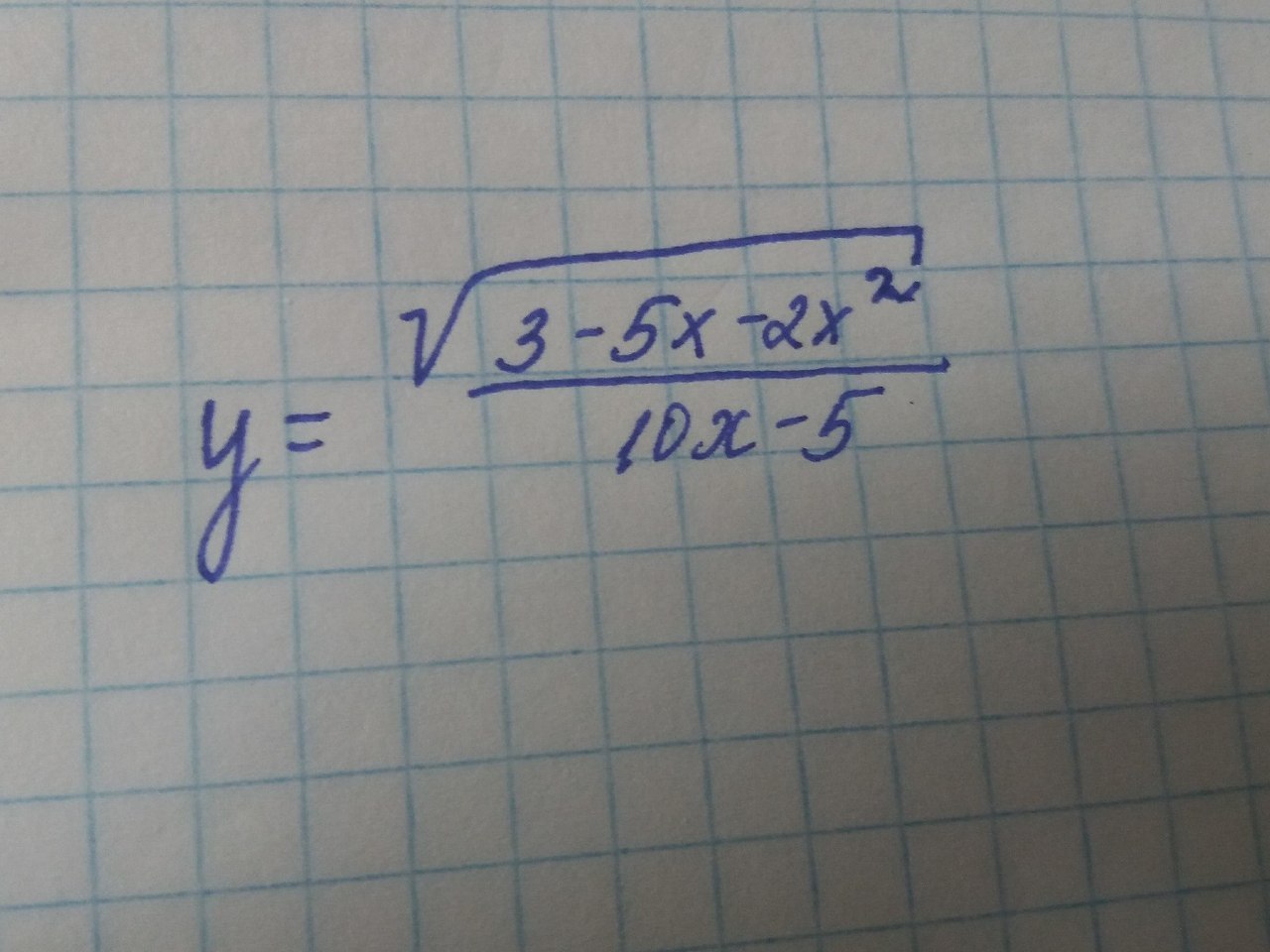
Ответы
Автор ответа:
2
Ответ: D(y) = [- 3; 1/2)
Объяснение:
Для нахождения области определения решим систему:
Решим первое неравенство:
2x² + 5x - 3 ≤ 0
D = 25 + 24 = 49
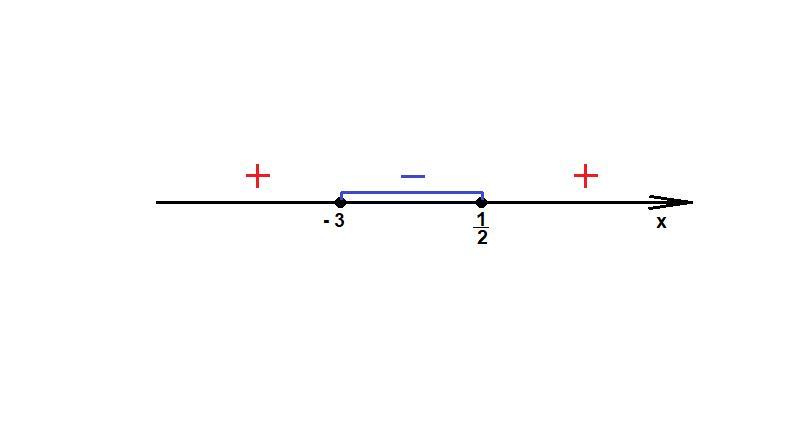
Отметим точки на координатной прямой, определим знаки выражения 2x² + 5x - 3 на интервалах (см. рис.)
x ∈ [- 3; 1/2]
D(y) = [- 3; 1/2)
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: jdjrmrkdok
Предмет: Алгебра,
автор: p4ramonovatatyana
Предмет: Физика,
автор: Marinajelezoglo81
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: fox12345fox