Question

В целиндре диагональ осевого сечения равна 8 см и составляет с плоскостью основания угол 30 градусов найти объём цилиндра

Answer 1

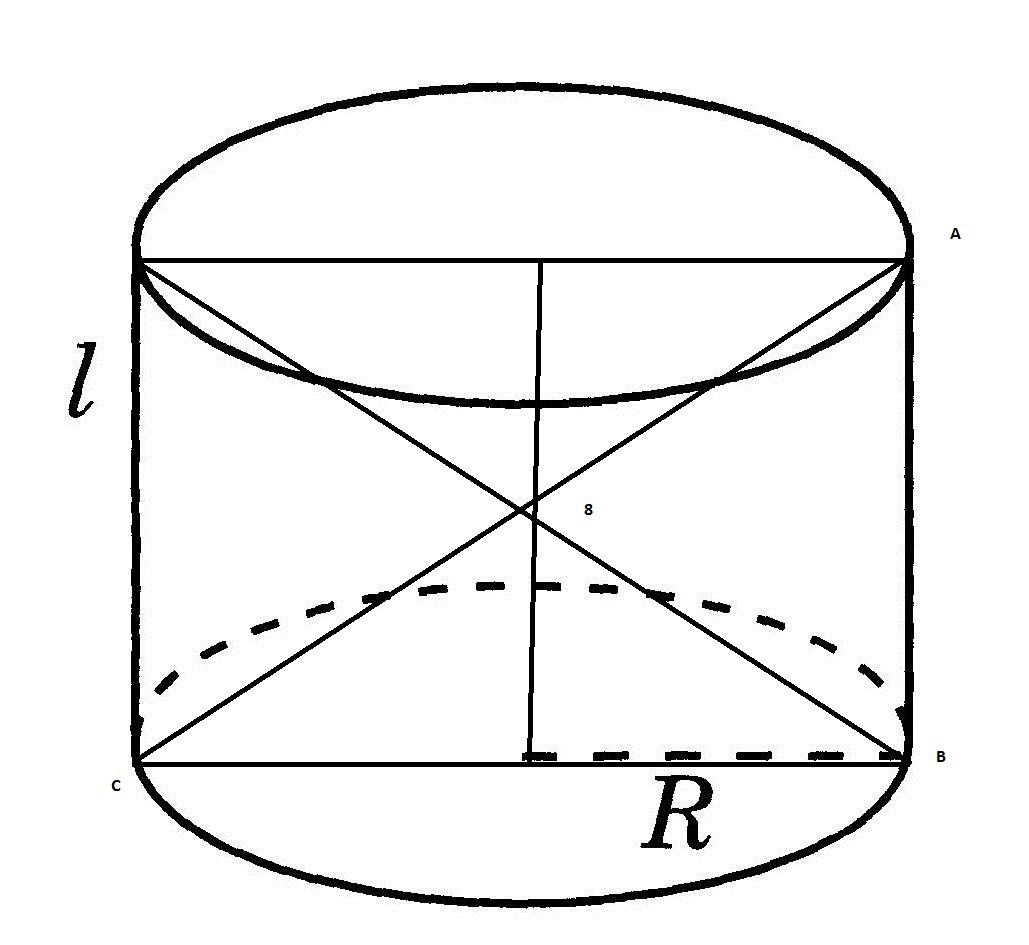
Осевое сечение цилиндра прямоугольник(его длина совпадает с образующей, а ширина с диаметром основания цилиндра). 
Диагональ в прямоугольнике делит его на два равных прямоугольных треугольника. В них известно по углу в 30* и общей гипотенузе в 8см.
Напротив угла в 30* в прямоугольном треугольнике находится катет равный половине гипотенузы. 8см/2= 4 см - мы нашли высоту цилиндра.
По теореме Пифагора найдём второй катет(диаметр основания)
$D=\sqrt{8^2-4^2}= \sqrt{64-16} = \sqrt{48}$
$r= \frac{D}{2}= \frac{\sqrt{48} }{2} = \frac{ 2\sqrt{12} }{2} =\sqrt{12}$
Объём цилиндра вычисляется по формуле:
$V=h*pi*r^2$
$V=4*pi* (\sqrt{12}) ^2$
$V=4*12*pi$
$V=48pi$