Предмет: Математика,
автор: mrandrew2014
Решите показательное уравнение по математике пожалуйста,буду благодарен,номер задания 26.
Приложения:
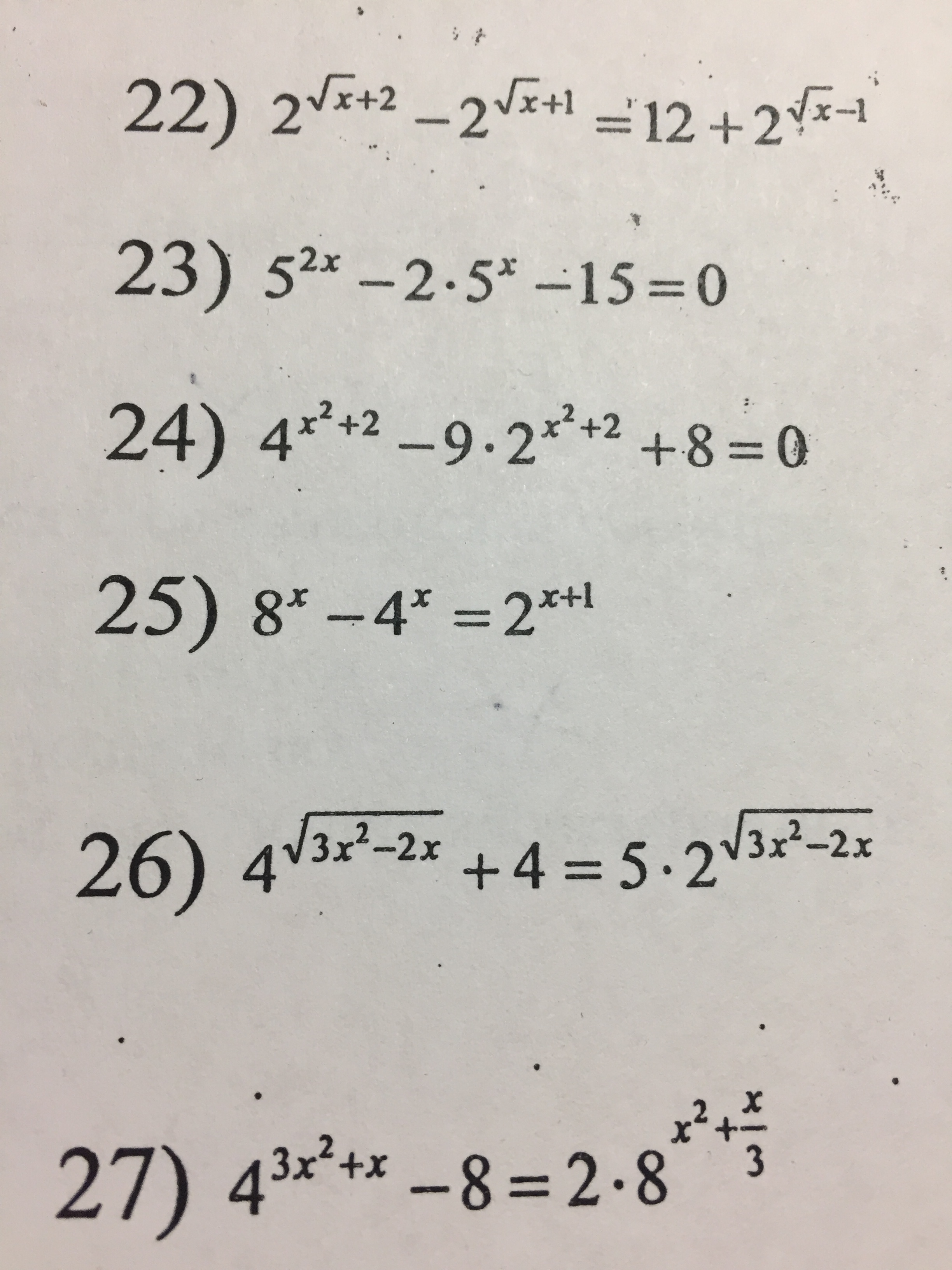
Ответы
Автор ответа:
1
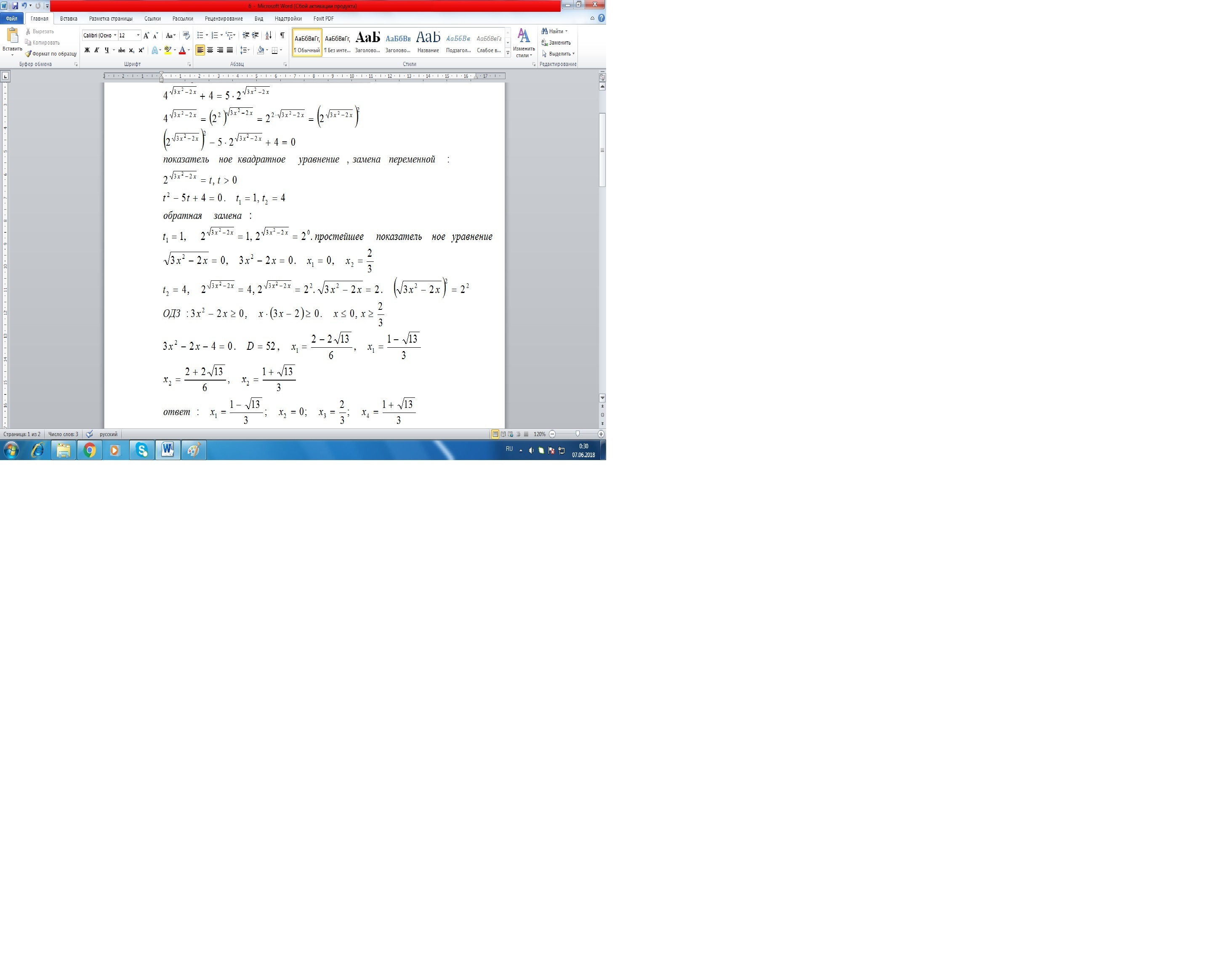
решение во вложении--------------
Приложения:
Аноним:
В ответе опечатка. Под корнем 13
спасибо. исправила
Автор ответа:
1
Похожие вопросы
Предмет: Английский язык,
автор: faraon2020
Предмет: Алгебра,
автор: user08191662919
Предмет: Математика,
автор: Moonlit89843
Предмет: Алгебра,
автор: natusikmik
Предмет: Математика,
автор: мапариаа