Предмет: Математика,
автор: Натали282
Помогите решить пожалуйста!Математика 10-11 класс
Приложения:
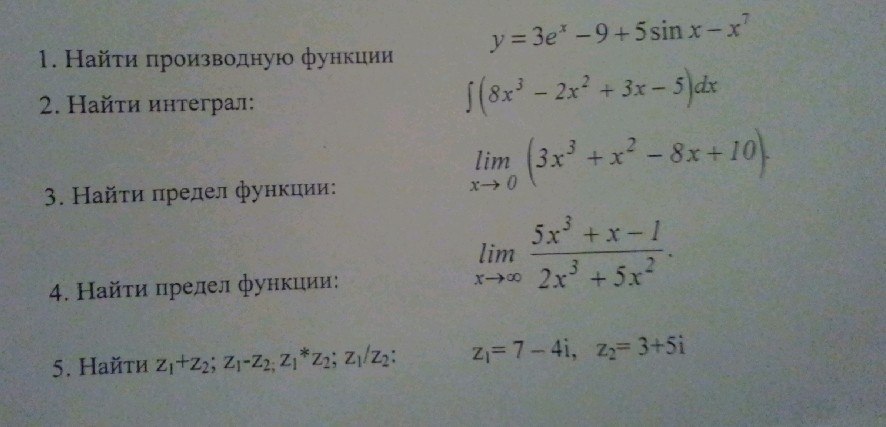
Ответы
Автор ответа:
1
1. y' = 3e^x + 5cosx - 7x^6 // производные элементарных функций
2. = 8x^4/4 - 2*x^3/3 + 3x^2/2 - 5x (интегралы элементарных функций)
3. lim (3x^3+x^2-8x+10) = 10 // подставляем x0, получается 10.
4. lim (5x^3+x-1)/(2x^3+5x^2) = lim (15x^2+1)/(6x^2+10x) = lim (30x)/(12x+10) = lim 30/12 = 30/12 = 5/2 // используем правило Лопиталя, т.е. берем производные, пока не избавимся от неопределенности (бесконечность/бесконечность)
5. z1+z2 = 10+i
z1-z2 = 4-9i
z1*z2 = (7 - 4i) · (3 + 5i) = 7·3 + 7·5i - 4·3i - 4·5i^2 = 21 + 35i - 12i + 20 = 41 + 23i
z1/z2 = (7 - 4i) / (3 + 5i) = (7-4i)*(3-5i)/(3+5i)(3-5i) = (7*3-7*5i-4*3i+4*5i^2)/(3^2 - (5i)^2) = (21-35i-12i-20)/(9+25) = (1-47i)/34 = 1/34 - 47/34 *i
2. = 8x^4/4 - 2*x^3/3 + 3x^2/2 - 5x (интегралы элементарных функций)
3. lim (3x^3+x^2-8x+10) = 10 // подставляем x0, получается 10.
4. lim (5x^3+x-1)/(2x^3+5x^2) = lim (15x^2+1)/(6x^2+10x) = lim (30x)/(12x+10) = lim 30/12 = 30/12 = 5/2 // используем правило Лопиталя, т.е. берем производные, пока не избавимся от неопределенности (бесконечность/бесконечность)
5. z1+z2 = 10+i
z1-z2 = 4-9i
z1*z2 = (7 - 4i) · (3 + 5i) = 7·3 + 7·5i - 4·3i - 4·5i^2 = 21 + 35i - 12i + 20 = 41 + 23i
z1/z2 = (7 - 4i) / (3 + 5i) = (7-4i)*(3-5i)/(3+5i)(3-5i) = (7*3-7*5i-4*3i+4*5i^2)/(3^2 - (5i)^2) = (21-35i-12i-20)/(9+25) = (1-47i)/34 = 1/34 - 47/34 *i
Натали282:
snow, можно просьбу? как у тебя все это получилось? решение 1-4?) спасибо;)
Похожие вопросы