Question

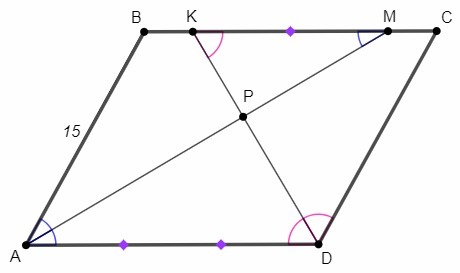
В параллелограмме ABCD биссектрисы углов А и D пересекают
сторону ВС в точках М и К соответственно, а отрезки АМ и DК пересекаются
в точке Р.
Найти длину стороны ВС, если известно, что АВ=15 и АР: РМ = 3:2.

Answer 1

В параллелограмме противоположные стороны параллельны и равны.

∠BAM=∠DAM (AM - биссектриса ∠BAD)
∠BMA=∠DAM (накрест лежащие при BC||AD)
∠BAM=∠BMA, △ABM - равнобедренный, AB=BM

Аналогично CD=CK

AB=CD => BM=CK => BK=CM

△APD~△MPK (по двум углам)
AD/MK=AP/PM =3/2

AD=BC =MK+2BK
MK= 2/3 AD => 2BK= 1/3 AD => AB =BK+MK =5/6 AD => BC= 6/5 AB =18