Предмет: Математика,
автор: egorkadv2002
Докажите, что если 1/a + 1/b + 1/c = 1/(a+b+c), то
1/a^3 + 1/b^3 + 1/c^3 = 1/(a^3 + b^3 + c^3)
Приложения:
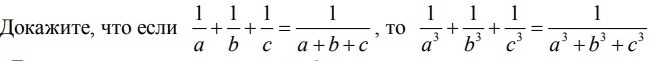
Ответы
Автор ответа:
1
Если a = -b, то утверждение очевидно.
Пусть a ≠ -b. Найдём c из первого равенства.
1/a + 1/b = 1/(a + b + c) - 1/c
(a + b)/(ab) = -(a + b)/(c (a + b + c)) – делим обе части уравнения на (a + b) ≠ 0
1/(ab) = -1/(c (a + b + c))
c^2 + (a + b) c + ab = 0
По теореме Виета сумма корней этого уравнения равна -(a + b), произведение ab. Очевидно, c = -a или c = -b. Но тогда опять-таки выполнение второго равенства очевидно.
Пусть a ≠ -b. Найдём c из первого равенства.
1/a + 1/b = 1/(a + b + c) - 1/c
(a + b)/(ab) = -(a + b)/(c (a + b + c)) – делим обе части уравнения на (a + b) ≠ 0
1/(ab) = -1/(c (a + b + c))
c^2 + (a + b) c + ab = 0
По теореме Виета сумма корней этого уравнения равна -(a + b), произведение ab. Очевидно, c = -a или c = -b. Но тогда опять-таки выполнение второго равенства очевидно.
rikarika55:
Помогите плиз
Нелии
https://znanija.com/task/29289079
Ээто оч важно прошу моя оценка зависит от этого плииз это последний номер в моих добавленных заданиях
https://znanija.com/task/29289079
Похожие вопросы
Предмет: Математика,
автор: privikpolystyrene
Предмет: Математика,
автор: sonamaksimova1
Предмет: Информатика,
автор: eva100237
Предмет: Алгебра,
автор: dasadasa0000