Предмет: Алгебра,
автор: sanyas322
решите пожалуйста!!!!!!!!!!!!!!!!!!!!!!
Приложения:
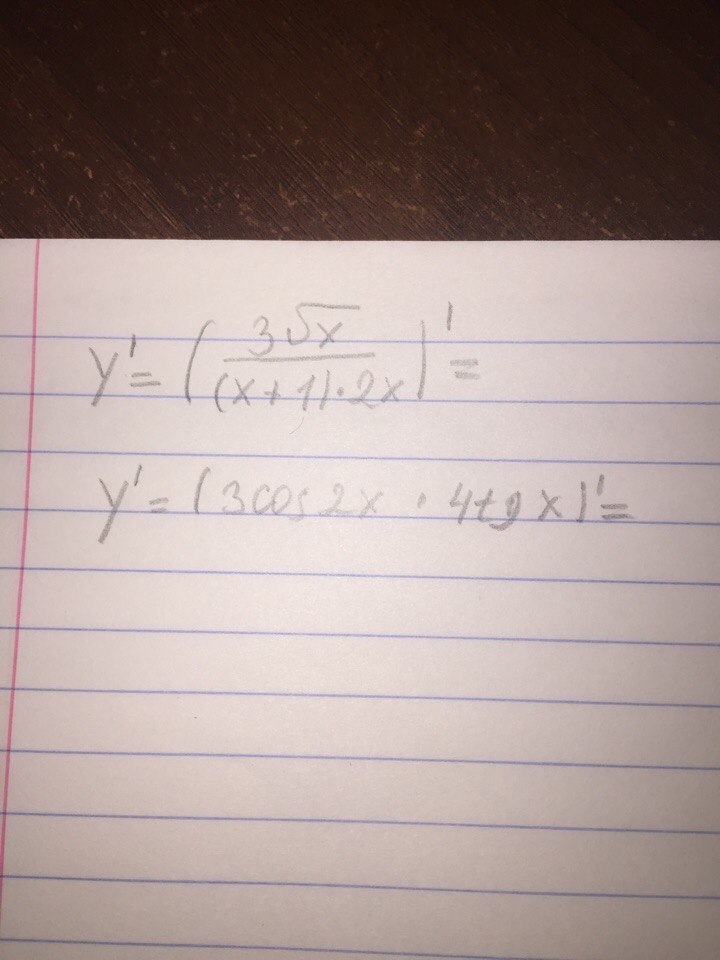
Ответы
Автор ответа:
0
1)

2)(3cos2x)'(4tgx)+3cos2x(4tgx)'=-6sin2x*4tgx+3cos2x* =-24*2sinxcosx*
=-24*2sinxcosx* +
+ =-48sin^2x+
=-48sin^2x+
по-братски дай лучший ответ я это 2 часа писал
2)(3cos2x)'(4tgx)+3cos2x(4tgx)'=-6sin2x*4tgx+3cos2x*
по-братски дай лучший ответ я это 2 часа писал
Похожие вопросы
Предмет: Математика,
автор: Maksim228557
Предмет: История,
автор: aangusejnova18
Предмет: Алгебра,
автор: ahmadalievasafina
Предмет: Математика,
автор: 20aishat04
Предмет: Математика,
автор: mfurman1424milka