Предмет: Математика,
автор: 75545
постройте график функции.при каких значениях М функция у=м имеет с графиком ровно 1 общую точку
Приложения:
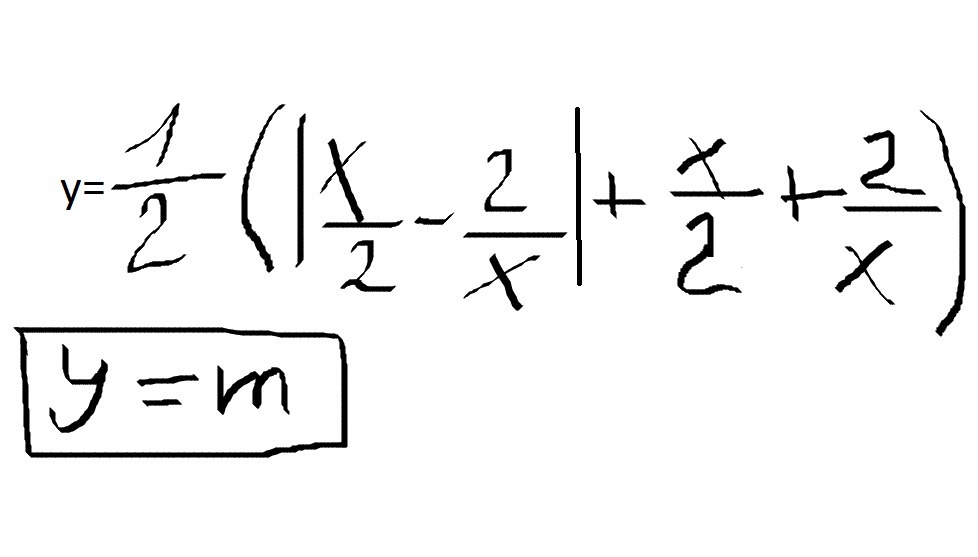
Ответы
Автор ответа:
0
Если  то решением этого неравенства есть:
то решением этого неравенства есть:

Последнее неравенство эквивалентно совокупности неравенств
На промежутке функция примет следующий вид:
функция примет следующий вид:
 - прямая, проходящая через начало координат.
- прямая, проходящая через начало координат.
Если , то функция примет следующий вид:
, то функция примет следующий вид:
 - гипербола (область определения - все значения х, кроме х=0)
- гипербола (область определения - все значения х, кроме х=0)
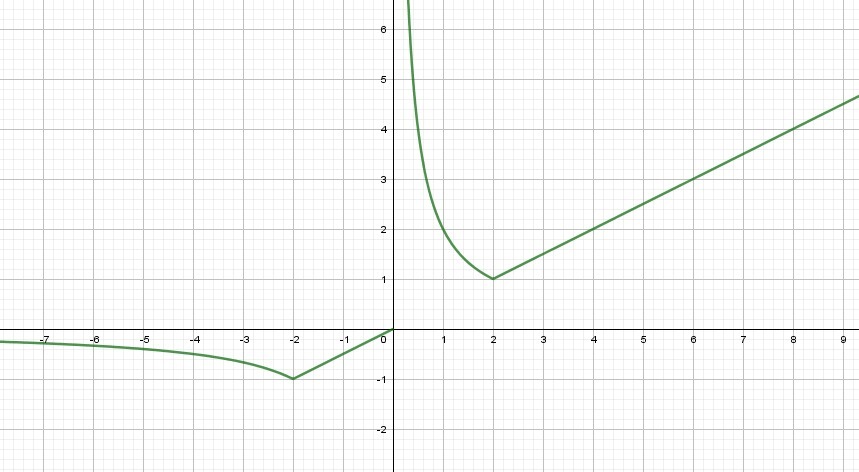
При m = ±1 графики пересекаются в одной точке
Последнее неравенство эквивалентно совокупности неравенств
На промежутке
Если
При m = ±1 графики пересекаются в одной точке
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: Anna228828281
Предмет: Русский язык,
автор: sorokinatatana749
Предмет: Литература,
автор: lalalaoz2020
Предмет: Литература,
автор: fanay
Предмет: Алгебра,
автор: kasfabfhhfhhfybr