Предмет: Математика,
автор: xoo1
Помогите пожалуйста решить 8й пример(желательно с описанием ходом решения)
Приложения:
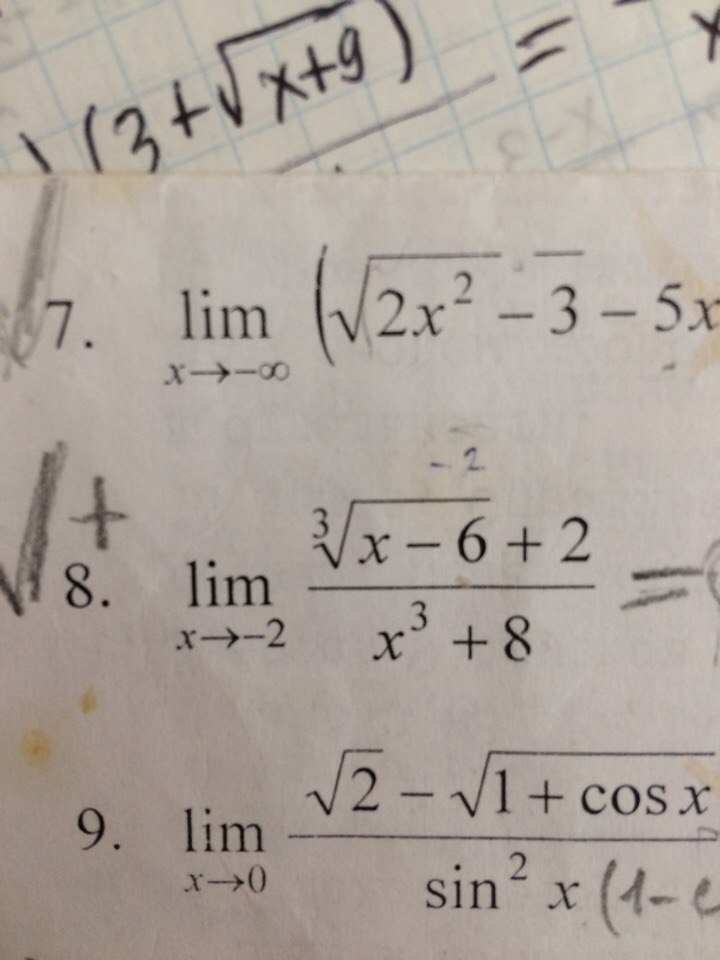
Ответы
Автор ответа:
2
знаменатель разложили по формуле суммы кубов и домножили числитель и знаменатель на множитель, чтобы в числителе получилась сумма кубов
xoo1:
Спасибо большое!!!
Похожие вопросы
Предмет: Английский язык,
автор: termolaevr
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: milkoann103
Предмет: Математика,
автор: егор552