Question

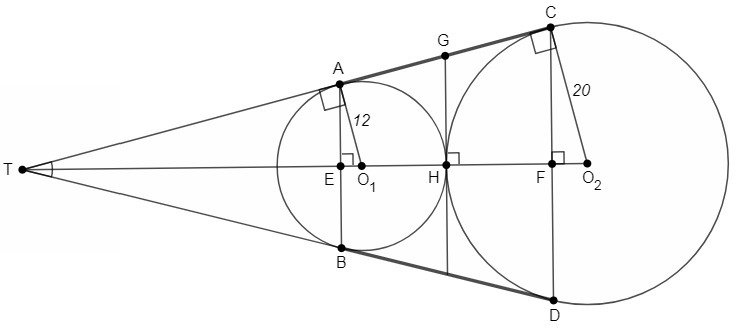
Окружности радиусов 12 и 20 касаютаются внешним образом. Точки А и В лежат на первой окружности точки С и D - на второй. При этом АС и ВD - общие касательные окружности. Найдите расстояние между прямыми АВ иСD

Answer 1

Общие касательные окружностей различных радиусов являются сторонами угла. Центры окружностей лежат на биссектрисе угла (так как окружности вписаны в угол). Отрезки касательных из одной точки равны, треугольники ATB и CTD равнобедренные, общая биссектриса является высотой, AB⊥TO₂, CD⊥TO₂, AB||CD.

Радиусы O₁A и O₂C перпендикулярны касательной AC, в треугольниках AO₁T и CO₂T угол при вершине T общий, ∠AO₁E=∠CO₂F. △AO₁E~△CO₂F по двум углам.

k=AO₁/CO₂ =12/20 =0,6
O₁E/O₂F =0,6

Через точку H проходит третья общая касательная, GH⊥TO₂. AG=GH, CG=GH (отрезки касательных из одной точки), AG=CG. GH параллельна AB и CD и делит EF в том же отношении, что и AC, то есть пополам, EH=FH.

EH=O₁H +O₁E =12+O₁E
FH=O₂H -O₂F =20-O₂F
12+O₁E = 20-O₂F <=> 0,6 O₂F= 8-O₂F <=> O₂F =8/1,6 =5

EF= 2FH =2(20-5) =30