Question

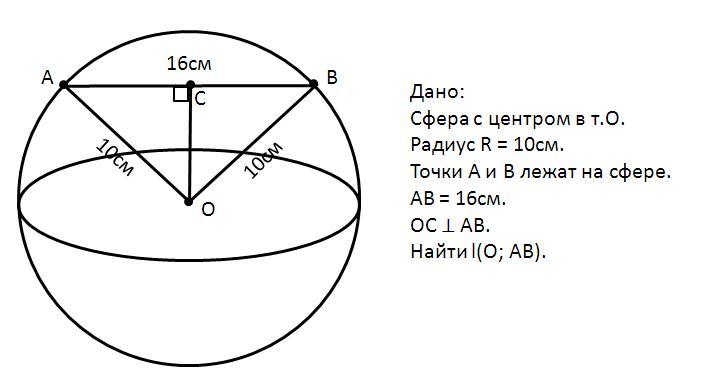
1. Точки А и B лежат на сфере радиус которой равен 10 см. Найти расстояние от центра сферы, до прямой АВ, если АВ=16см.

Answer 1

Ответ:

Расстояние от центра сферы до прямой АВ равно 6 см.

Объяснение:

• Расстояние от точки до прямой равно длине перпендикуляра, опущенного из точки на прямую.

ОС ⊥ АВ ⇒ l(O; АВ) = ОС.

• Радиус сферы – это расстояние, на которое каждая точка удалена от центра сферы.

О - центр сферы, точки А и B лежат на сфере ⇒ ОА = ОВ = R = 10см.

• Если у треугольника две стороны равны, то этот треугольник — равнобедренный.

ОА = ОВ ⇒ ΔОАВ - равнобедренный.

• Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону.

ОС ⊥ АВ ⇒ ОС - высота ΔОАВ.

• В равнобедренном треугольнике высота является и биссектрисой, и медианой.

ΔОАВ - равнобедренный, ОС - высота ΔОАВ ⇒ ОС - медиана и биссектриса ΔОАВ.

• Медиана треугольника ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

ОС - медиана ΔОАВ ⇒ АС = СВ = АВ : 2 = 16 : 2 = 8см.

• Теорема Пифагора — в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.

Рассмотрим ΔАСО - прямоугольный (т.к. ОС ⊥ АВ).

По теореме Пифагора АО²=АС²+ОС², отсюда:

$\displaystyle OC = \sqrt{AO^2-AC^2} =\sqrt{10^2-8^2} =\sqrt{100-64}=\sqrt{36}=6\text{cm}$

Как мы уже выяснили, ОС - расстояние от центра сферы до прямой АВ, тогда расстояние от центра сферы до прямой АВ равно 6 см.

#SPJ5