Question

решение графика
$y = \frac{(0.75 {x}^{2} + 1.5x) \times |x| }{x + 2}$
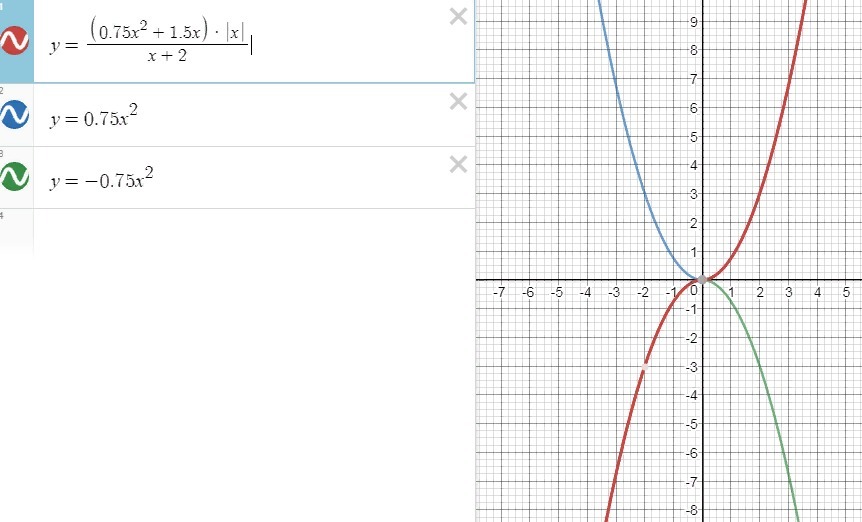
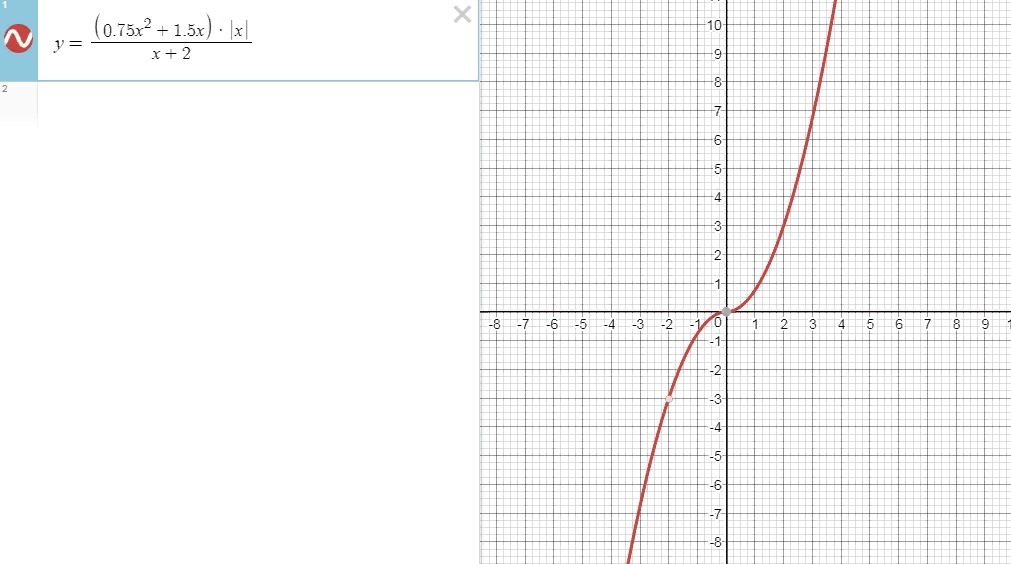
построить график и определить при каких значениях m прямая y=m не имеет с графиком ни одной общей точки

Answer 1

$y = \frac{(0.75 {x}^{2} + 1.5x) \times |x| }{x + 2} = \frac{0.75x(x+2) \times |x| }{x + 2} = 0.75x|x| \\ \\ 1)y=0.75x^2$
парабола, ветви вверх, берем ту часть ,где х≥0 
$2)y=-0.75x^2$
парабола, ветви вниз, берем ту часть ,где х<0  

график красного цвета
выколотая точка х=-2
y(-2)=-0.75*(-2)^2=-3/4*4=-3
m=-3

прямая y=-3 не имеет  с графиком ни одной общей точки