Question

как в задаче;Картинка имеет форму прямоугольника со сторонами 11 см и 16 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 300 см2. Какова ширина окантовки? Ответ дайте в сантиметрах. получается 496

Answer 1

Ширина окантовки  k см . 
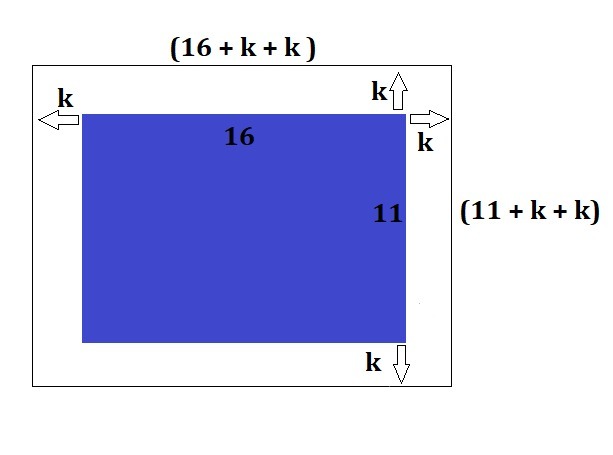
Площадь картины с окантовкой (см. приложение) :
(16 + k + k)×(11 + k + k)  = 300  
( 16 + 2k )×( 11 + 2k) = 300
16 × 11 + 16×2k  + 2k×11 + 2k×2k  = 300
176 + 32k  + 22k   + 4k²  = 300
4k² + 54k  + 176  - 300  = 0
4k²  + 54k   - 124 = 0
2×(2k²  + 27k  - 62) = 0            |÷2
2k²  + 27k  - 62  = 0
D = 27² - 4×2×(-62) = 729 +496 = 1225 = 35²
D>0 - два корня уравнения
k₁ =  ( - 27  - 35)/(2×2) = -62/4 = - 15,5  - не удовлетворяет условию задачи, т.к. ширина - неотрицательная величина.
k₂ = ( - 27 + 35) / (2×2) = 8/4 = 2  (см)  ширина окантовки

Ответ:  2 см.
Не получается  496....