Question

Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 135°, а CD=29

Answer 1

Ответ:

AB = 29√2

Объяснение:

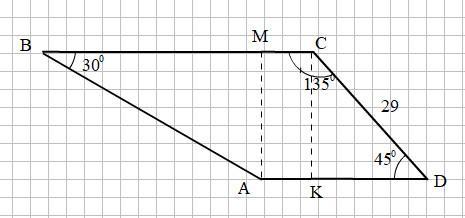
Смотри рисунок на прикреплённом фото.

∠ВСD = 135°. Односторонний с ним ∠ADC = 180° - 135° = 45°

В прямоугольном ΔKCD: ∠KCD = 90° - ∠ADC =  90° - 45° = 45° и ΔKCD равнобедренный с основанием CD.

Тогда KD = CK = CD · cos 45° = 29/√2

АM и СК - высоты трапеции, поэтому они равны, то есть

АМ = СК = 29/√2

В прямоугольном  Δ АВМ катет АМ лежит против угла АВM, равного 30°, значит АВ = 2 · АМ = 2 · 29/√2 = 29√2