Предмет: Алгебра,
автор: zakokuvi
cot²x=? Напишите формулу и напишите решение для задания 71.
СДЕЛАЙТЕ ТО ЧТО Я ПОПРОСИЛ!!!
Приложения:

Ответы
Автор ответа:
0
___________________________
Приложения:

Godnessgirl:
=cos²x/sin²x
это в моем ответе
Самый последний пункт где ты нашла x1,x2 не понял.
х1 для sinx=1, x2 для sinx=-1
3=2sinx²+sinx²+сosx² тоже не понятно.
3sin²x=2sin²x+1sin²x
Объединение не понятно.х=Π/2+Πn? Где перед пи 2? Почему его нет?
его нет, потому чио бы получит -π/2 с π/2 к нему нужно прибавить π, а не 2π
извиняюсь , но почему у нас разные ответы , методы решения отличны , но конечный результат тоже
сделай проверку своим ответам
Автор ответа:
0
sin²x≠0
sinx≠0
x≠πn, nєZ

умножим на sin²x, получим

по основному тригонометрическому тождеству

значит

получим систему
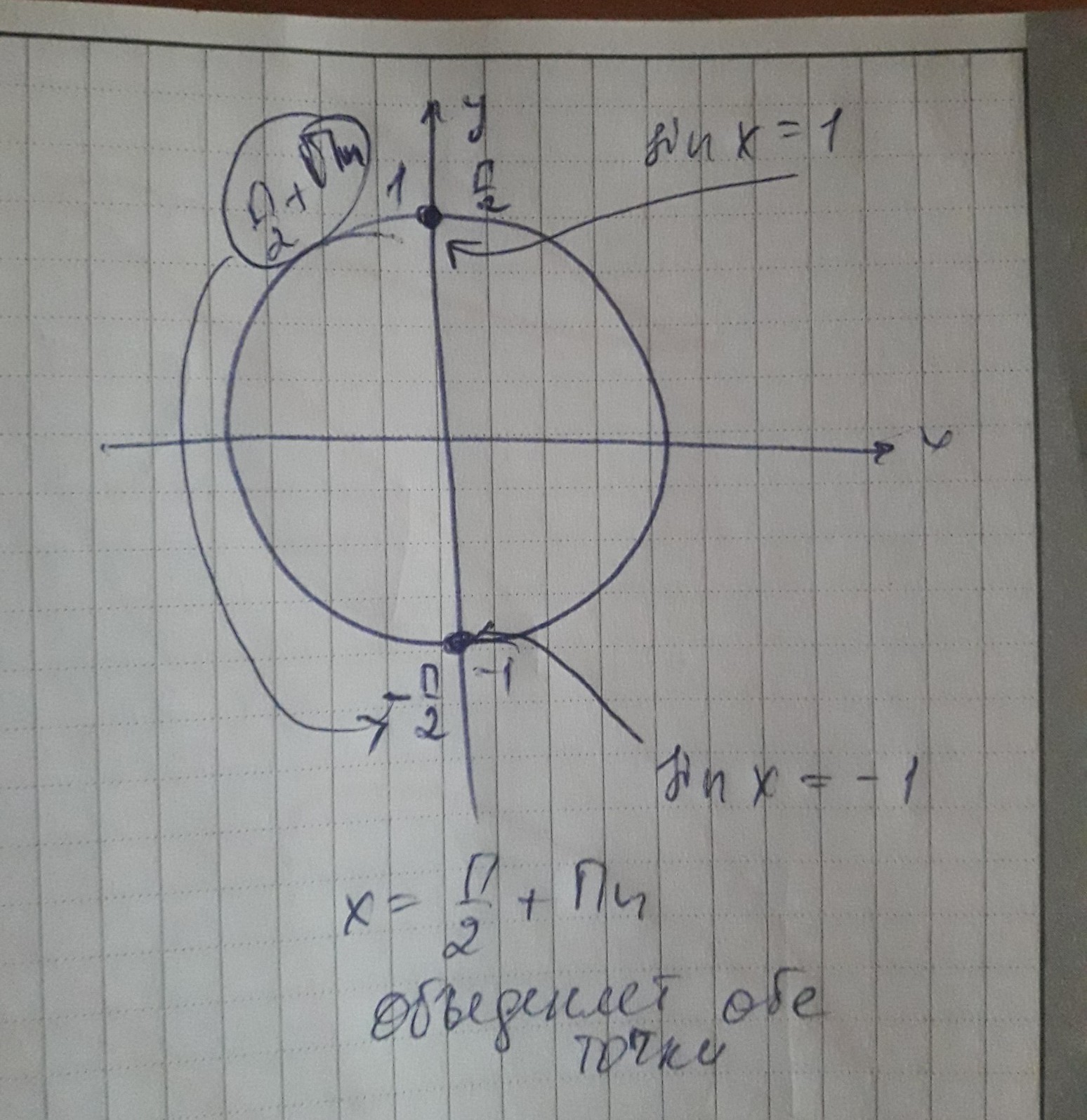
sinx=1 или sinx=-1
х1=π/2 + 2πn, nєZ
х2=-π/2 + 2πn, nєZ.
если объединить а один ответ, то получим
х=π/2 + πn, nєZ.
ответ:Е
sinx≠0
x≠πn, nєZ
умножим на sin²x, получим
по основному тригонометрическому тождеству
значит
получим систему
sinx=1 или sinx=-1
х1=π/2 + 2πn, nєZ
х2=-π/2 + 2πn, nєZ.
если объединить а один ответ, то получим
х=π/2 + πn, nєZ.
ответ:Е
Приложения:
Похожие вопросы
Предмет: Химия,
автор: danya643rus
Предмет: Математика,
автор: jimmxxwii
Предмет: Алгебра,
автор: abzalovtimur04
Предмет: Геометрия,
автор: НютаСтолярова