Question

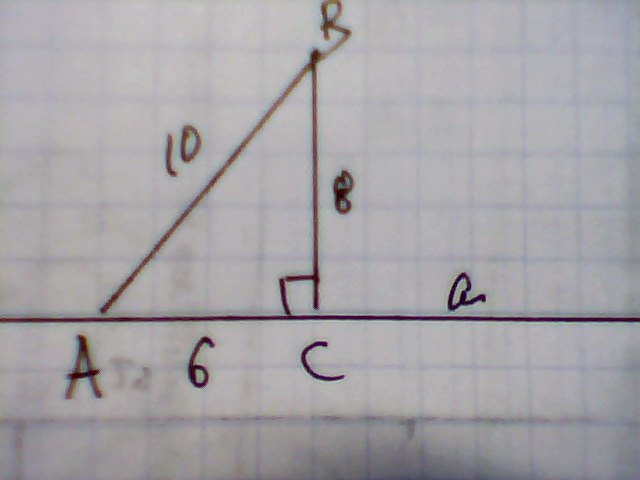
1) Наклонная длиной 10см, проведенная из данной точки к прямой, имеет проекцию длиной 6см. Вычислите длину перпендикуляра, опущенного из этой точки на прямую.
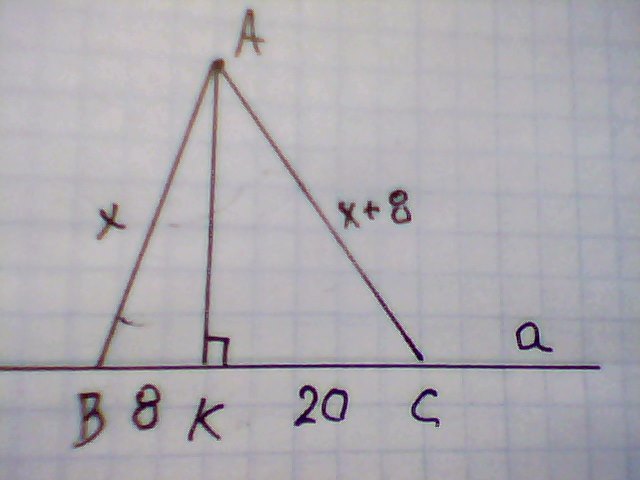
2) Из точки к прямой проведены перпендикуляр и две наклонные, разность длин которых составляет 8см. Найдите длину перпендикуляра, если проекции наклонных равны 8см и 20см.

Answer 1

1) АВ- наклонная равная 10 см, ЕЕ проекция на прямуа равна АС=6 см. 
ВС²=АВ²+АС²=10²-6²=100-36=64; ВС=√64=8 см.
2) По условию АК⊥а,  ВК=8 см;СК=20 см Определить АК.
ΔАВК. Пусть АВ=х.
АК²=АВ²-ВК²=х²-8²=х²-64.
ΔАСК. По условию АС=х+8; АК²=АС²-СК²=(х+8)²-20²=х²+16х+64-400.
х²-64=х²+16х-336
16х=272; х=272/16=17;  АВ=17 см;  АС=17+8=25 см