Предмет: Геометрия,
автор: KavboyClap
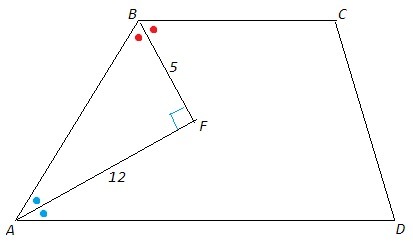
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F Найдите AB если AF равно 12 BF равно 5
Ответы
Автор ответа:
11
Сумма углов, прилежащих боковой стороне трапеции, равна 180°. Следовательно сумма половин этих углов равна 90°. Треугольник, образованный биссектрисами и боковой стороной - прямоугольный.
AB - боковая сторона трапеции; AF, BF - биссектрисы.
∠A+∠B=180° (односторонние углы при параллельных)
∠A/2 +∠B/2 =90°
∠AFB= (180°-(∠A/2 +∠B/2)) =180°-90° =90°
AB=√(AF^2 +BF^2) =√(12^2 +5^2) =13
AB - боковая сторона трапеции; AF, BF - биссектрисы.
∠A+∠B=180° (односторонние углы при параллельных)
∠A/2 +∠B/2 =90°
∠AFB= (180°-(∠A/2 +∠B/2)) =180°-90° =90°
AB=√(AF^2 +BF^2) =√(12^2 +5^2) =13
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: m5nazart
Предмет: Математика,
автор: kanamatovainaja
Предмет: История,
автор: ceburekedinogovyj
Предмет: Математика,
автор: IlyaNPP
Предмет: Математика,
автор: HOSHKA