Предмет: Математика,
автор: marintseva2000
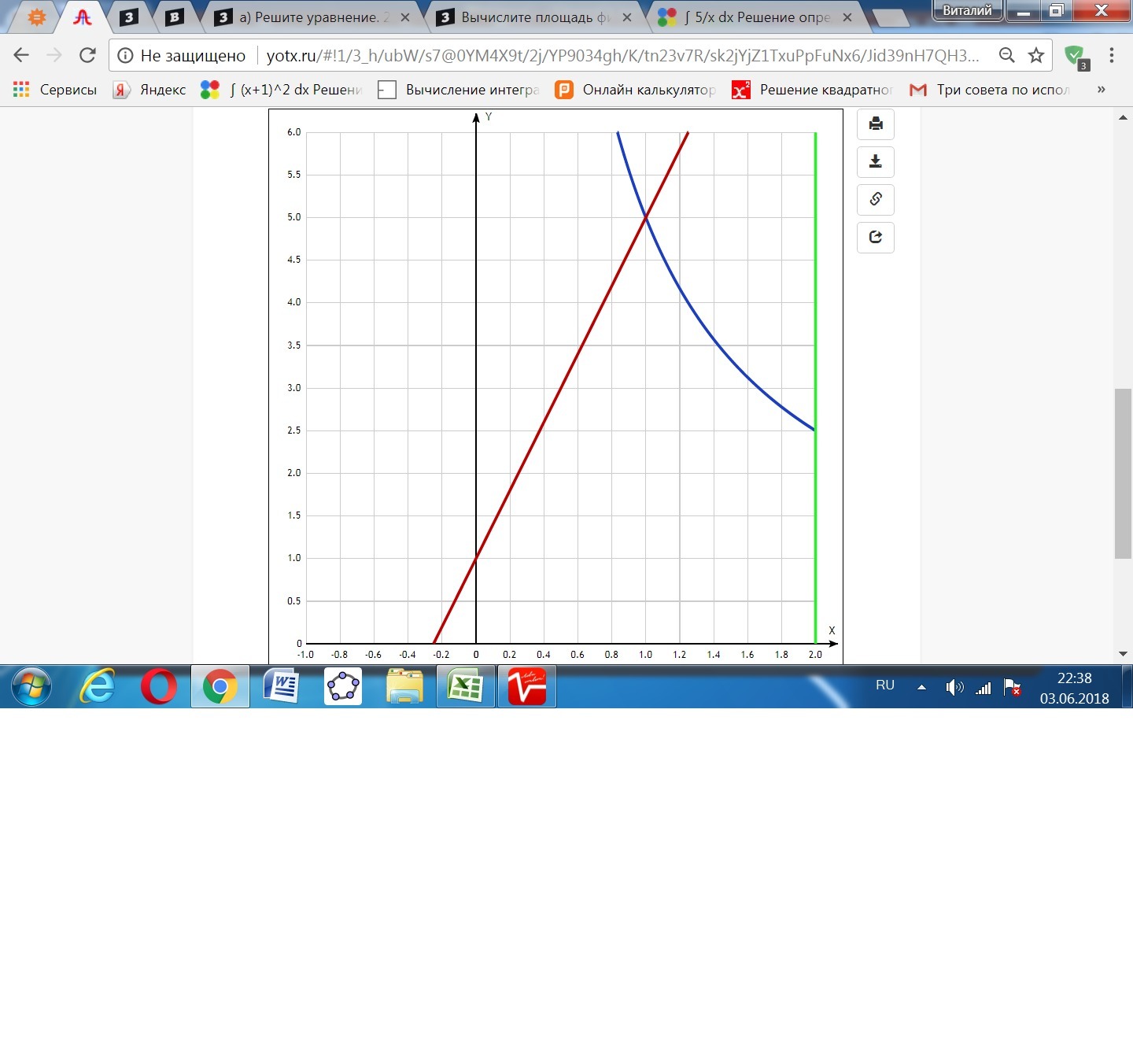
Вычислите площадь фигуры, ограниченной гиперболой у = 5/х и прямыми у = 4х + 1 и х = 2.
Ответы
Автор ответа:
4
Фигура, ограниченная гиперболой у = 5/х и прямыми у = 4х + 1 и х = 2 (с дополнительным условием у = 0), представляет собой треугольник и криволинейную трапецию.
Находим крайнюю левую точку - пересечение прямой с осью Ох.
4х +1 = 0, х = -1/4 = -0,25.
Находим точку пересечения прямой и гиперболы.
5/х = 4х + 1. Получаем квадратное уравнение:
4х² + х - 5 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1^2-4*4*(-5)=1-4*4*(-5)=1-16*(-5)=1-(-16*5)=1-(-80)=1+80=81;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√81-1)/(2*4)=(9-1)/(2*4)=8/(2*4)=8/8=1;x_2=(-√81-1)/(2*4)=(-9-1)/(2*4)=-10/(2*4)=-10/8=-1,25. Это значение не принимаем - это точка пересечения с гиперболой в третьей четверти.
Ордината точки пересечения у = 5/1 = 5.
Находим площадь первой части фигуры:
S1 = (1/2)*(1+0,25)*5 = 3,125 кв.ед.
Площадь второй части равна интегралу: интеграл от произведения функции на константу есть эта константа на интеграл от данной функции.

Общая площадь равна 6,59074 кв.ед.
Находим крайнюю левую точку - пересечение прямой с осью Ох.
4х +1 = 0, х = -1/4 = -0,25.
Находим точку пересечения прямой и гиперболы.
5/х = 4х + 1. Получаем квадратное уравнение:
4х² + х - 5 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=1^2-4*4*(-5)=1-4*4*(-5)=1-16*(-5)=1-(-16*5)=1-(-80)=1+80=81;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√81-1)/(2*4)=(9-1)/(2*4)=8/(2*4)=8/8=1;x_2=(-√81-1)/(2*4)=(-9-1)/(2*4)=-10/(2*4)=-10/8=-1,25. Это значение не принимаем - это точка пересечения с гиперболой в третьей четверти.
Ордината точки пересечения у = 5/1 = 5.
Находим площадь первой части фигуры:
S1 = (1/2)*(1+0,25)*5 = 3,125 кв.ед.
Площадь второй части равна интегралу: интеграл от произведения функции на константу есть эта константа на интеграл от данной функции.
Общая площадь равна 6,59074 кв.ед.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vitaminkazaminka
Предмет: Українська література,
автор: nikitacuba673
Предмет: Математика,
автор: timuribragimzade
Предмет: Математика,
автор: анна500