Question

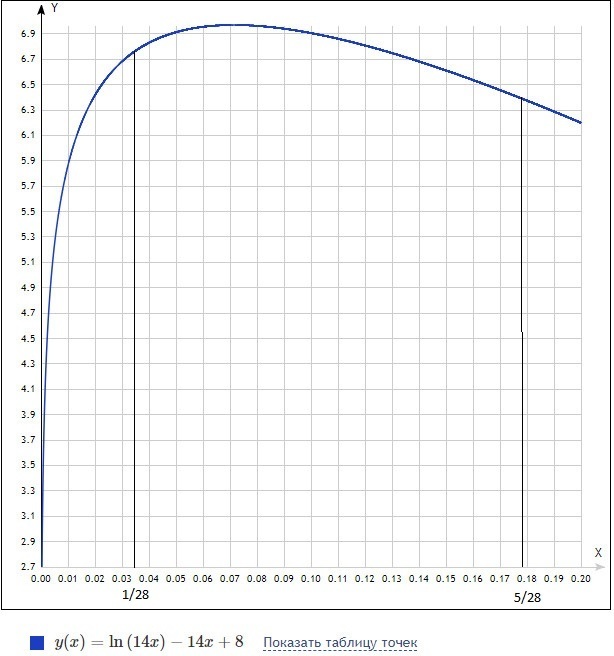
Найти точку минимума y=ln(14x)-14x+8
На промежутке [1/28;5/28]

Answer 1

Найти точку минимума y=ln(14x)-14x+8 На промежутке [1/28;5/28] 

Решение
Область определения функции х>0.
Найдем производную функции
y' = (ln(14x)-14x+8)' =(ln(14x)' -(14x)' +8' = (1/(14x))*(14x)' -14 =         
    = (1/(14x))*14 - 14 = 1/x -14 = (1 - 14x)/x
Найдем критические точки приравняв производную к нулю
                    y' = 0
            (1 - 14x)/x = 0
               1 -  14x = 0
                        x = 1/14
Точка х =1/14 входит в исследуемый промежуток [1/28;5/28]
На числовой прямой отображаем эту точку и знаки производной полученной по методу подстановки. Например при х =1 производная 
y'(1) =(1-14*1)/1 =-13<0
        +              0                -
---------------------!---------------------
                       1/14
Функция возрастает на интервале (0;1/14)
Функция убывает на интервале (1/14;+oo)
В точке х=1/14 функция имеет локальный максимум.
Найдем значения функции на границах исследуемого отрезка
х=1/28
y(1/28) = ln(14*1/28) - 14*1/28 + 8 = ln(1/2) - 1/2 + 8 = 7,5 - ln(2) ≈ 6,807
х=5/28
y(5/28) = ln(14*5/28) - 14*5/28 + 8 = ln(5/2) - 5/2 + 8 = 5,5 + ln(2,5) ≈ 6,416

Поэтому функция y=ln(14x)-14x+8 на промежутке [1/28;5/28] имеет минимальное значение в точке х =5/28   y(5/28) = 5,5 + ln(2,5) ≈ 4,416

Ответ:ymin = 5,5 + ln(2,5) ≈ 6,416