Предмет: Алгебра,
автор: pindaks
Умоляю помогите с решением дифференциального уравнения первого порядка
Приложения:
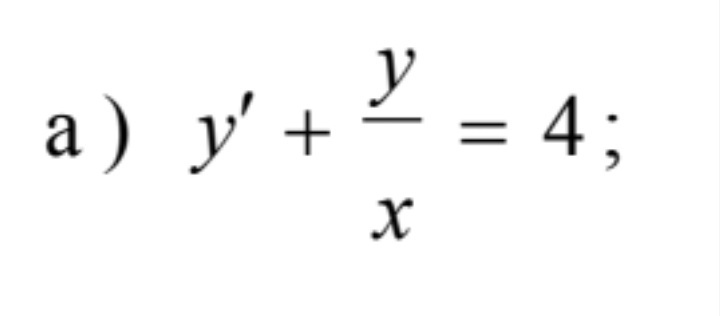
Ответы
Автор ответа:
0
Ответ:
Приложения:
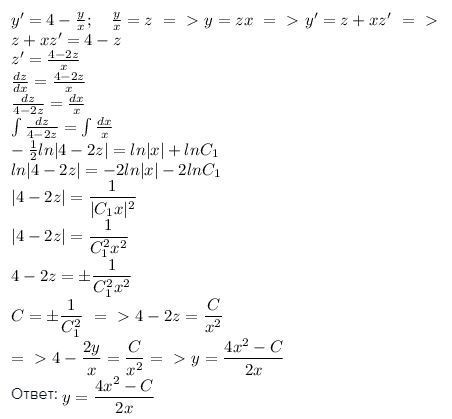
pindaks:
Что такое z ?
z - это подстановка в уравнение новой переменной вместо дроби у/х
Похожие вопросы
Предмет: Математика,
автор: pomoranton4
Предмет: Математика,
автор: Adilet1756
Предмет: Русский язык,
автор: korneevets
Предмет: Математика,
автор: Dianhik1