Предмет: Геометрия,
автор: valera159156
Подскажите пожалуйста---------Один из острых углов прямоугольного треугольника равняется 32 градуса Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла треугольника
Ответы
Автор ответа:
3
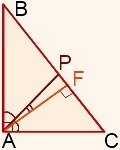
1) Так как AP — биссектриса прямого угла A, то ∠BAP=∠CAP=45º.
2) Найдем второй острый угол: 180-(90+32) = 180-122 = 58°
3) Найдем ∠BPA: 180-(∠BAP+∠B) = 180-(45+32) = 180-77 = 103°
4) Найдем смежный с предыдущим углом угол: ∠FPA = 180-∠BPA = 180-103 = 77
5) Так как ∠AFC=90°, то смежный с ним ∠AFP будет тоже 90°
Откуда получаем, что ∠PAF = 180-(∠APF+∠AFP) = 180-(77+90) = 180-167 = 13°
Ответ: 13°
2) Найдем второй острый угол: 180-(90+32) = 180-122 = 58°
3) Найдем ∠BPA: 180-(∠BAP+∠B) = 180-(45+32) = 180-77 = 103°
4) Найдем смежный с предыдущим углом угол: ∠FPA = 180-∠BPA = 180-103 = 77
5) Так как ∠AFC=90°, то смежный с ним ∠AFP будет тоже 90°
Откуда получаем, что ∠PAF = 180-(∠APF+∠AFP) = 180-(77+90) = 180-167 = 13°
Ответ: 13°
Приложения:
Похожие вопросы
Предмет: Математика,
автор: incierika
Предмет: Геометрия,
автор: aleshkinav04
Предмет: Русский язык,
автор: lyudmila1782
Предмет: Литература,
автор: Statica
Предмет: Биология,
автор: skrыTnый