Предмет: Математика,
автор: Valley00
Тригонометрическое уравнение. Номер 13 в ЕГЭ по профильной математике.
а) найдите корни уравнения
б) найдите корни, принадлежащие данному промежутку
Приложения:
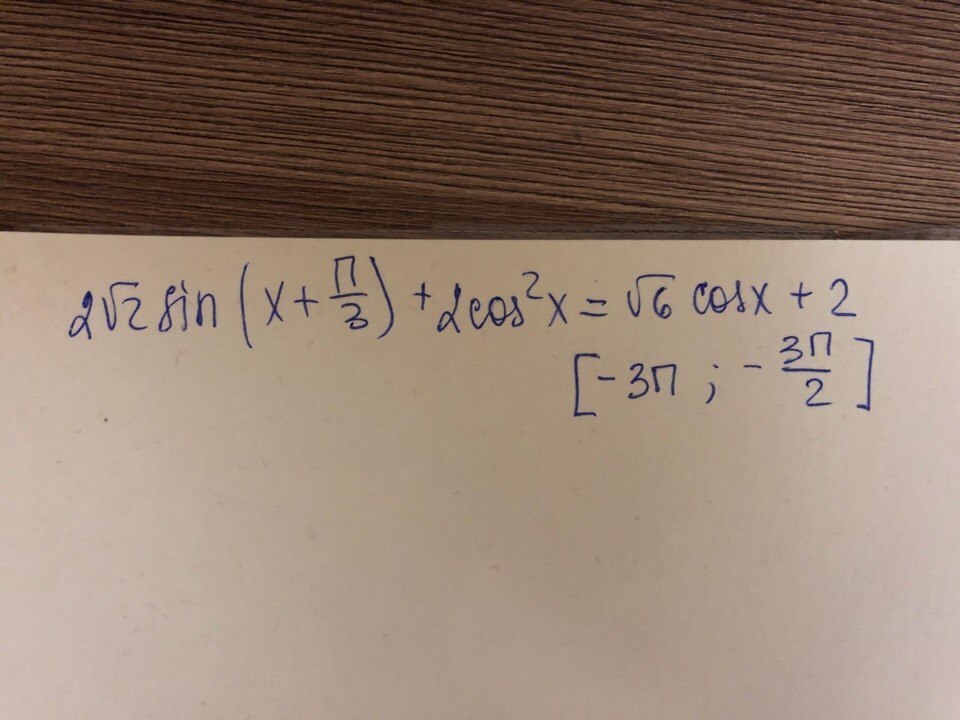
Ответы
Автор ответа:
5
на промежутке [-3π; -3π/2]
-3π; -2π; -2π+π/4=-7π/4
Ответ :
а) πn; π/4+2πn; 3π/4+2πn; n∈Z
b) -3π; -2π; -7π/4
Автор ответа:
10
Решение дано на фото.
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: lesi4ka6
Предмет: Математика,
автор: Vera12343211232
Предмет: Геометрия,
автор: costles