Предмет: Алгебра,
автор: Аноним
Найти угол в уравнении. 100 балов

Уравнение сложное. Должно быть два значения.
Подсказка: Сведите задачу к квадратному уравнению относительно tgα, воспользовавшись основным тригонометрическим тождеством.
Пробовал свести - не получается.
На всякий случая прикладываю ответ (см. рисунок)
Приложения:
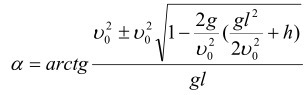
Ответы
Автор ответа:
1
Воспользовавшись тождеством
1+tg^2a=1/cos^2a
Подставляя
h=tga*L - g*L^2*(1+tg^2a)/(2v^2)
Или
(-g*L^2/(2v^2))*tg^2a + L*tga - (g*L^2/(2v^2)+h) = 0
Получили квадратное уравнение
D=sqrt(L^2-(4*g*L^2/(2v^2))*(g*L^2/(2v^2)+h)) = L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h))
tga=(-L+/- L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h)))/(-g*L^2/v^2)
Откуда сокращая на L , умножая числитель на v^2 , получаем требуемое
1+tg^2a=1/cos^2a
Подставляя
h=tga*L - g*L^2*(1+tg^2a)/(2v^2)
Или
(-g*L^2/(2v^2))*tg^2a + L*tga - (g*L^2/(2v^2)+h) = 0
Получили квадратное уравнение
D=sqrt(L^2-(4*g*L^2/(2v^2))*(g*L^2/(2v^2)+h)) = L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h))
tga=(-L+/- L*sqrt(1-(2*g/v^2)*(g*L^2/(2v^2)+h)))/(-g*L^2/v^2)
Откуда сокращая на L , умножая числитель на v^2 , получаем требуемое
Матов:
На пользу
Здравствуйте! Очень прошу посмотреть Мат. ожидание стратегия игры
https://znanija.com/task/29274828
https://znanija.com/task/29274828
Похожие вопросы
Предмет: Английский язык,
автор: naletovacc
Предмет: Геометрия,
автор: Аноним
Предмет: Химия,
автор: zarskaaanna41
Предмет: Математика,
автор: lenavika2014k
Предмет: Математика,
автор: Прохожийсулицы