Предмет: Алгебра,
автор: zumratzum
решите пожалуйста неравенство методом интервалов
Приложения:
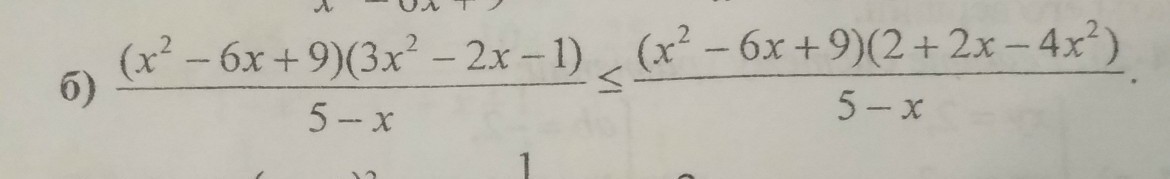
Ответы
Автор ответа:
1
- + - - +
-----|------|-----|------o---->x
Ответ:
Приложения:
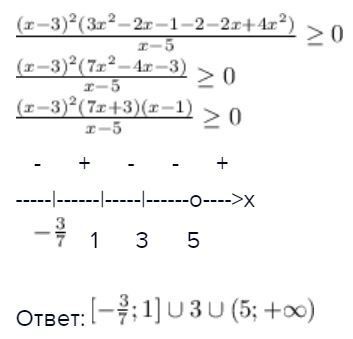
zumratzum:
это госовские задания специально составленные от министерства образования и науки государства
ок
вот можете сказать почему х-5 местами поменялись
так удобнее потом знаки определять на интервалах. поменял знак в (5-х) и синхронно с этим изменил знак самого неравенства
аа спасибо
на здоровье
а так правильно будет? ничего не изменится если изменить знак в самом неравенстве
без причины, а только по желанию знак неравенства менять нельзя. изменится как минимум выбор интервалов в ответ
можете без изменений попробовать ааа
всее спасибооо большое, сама справилась))
Похожие вопросы
Предмет: Геометрия,
автор: damianstojkovic0
Предмет: Физика,
автор: kitkitzelen
Предмет: Русский язык,
автор: zenagulkina4
Предмет: Информатика,
автор: JGHDBJ423