Предмет: Геометрия,
автор: savostyaneugen
Решите задачу с пояснениями пожалуйста.
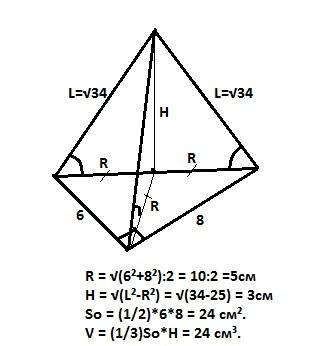
все боковые ребра треугольной пирамиды составляют с основанием равные углы, а основанием пирамиды является прямоугольный треугольник с картами 8 и 6 см. найти объём пирамиды, если длина бокового ребра пирамиды равна √34 см
Ответы
Автор ответа:
3
Ответ:
V = 24 см³.
Объяснение:
Так как все боковые ребра треугольной пирамиды составляют с основанием равные углы, то вершина пирамиды будет проецироваться в центр описанной около основания пирамиды окружности.
В прямоугольном треугольнике (основание пирамиды) этот центр расположен в середине гипотенузы. Радиус описанной окружности равен половине гипотенузы , то есть R=√(8²+6²)/2 = 5см (по Пифагору).
Тогда высоту Н пирамиды можно найти по теореме Пифагора из треугольника, образованного радиусом описанной окружности, высотой пирамиды (катеты) и боковым ребром (гипотенуза).
Н = √((√34)²-5²) = 3см.
Объем пирамиды равен V = (1/3)·So·H
So = (1/2)·6·8 = 24 см² (площадь основания - прямоугольного треугольника).
V = (1/3)·24·3 = 24 см³.
Приложения:
Похожие вопросы
Предмет: История,
автор: kilssjsnn
Предмет: Математика,
автор: elweniskenderov87544
Предмет: Математика,
автор: yusifhuseynov91000
Предмет: Математика,
автор: aidaagrba