Предмет: Математика,
автор: BJIADA
Помогите решить неравенство
Приложения:
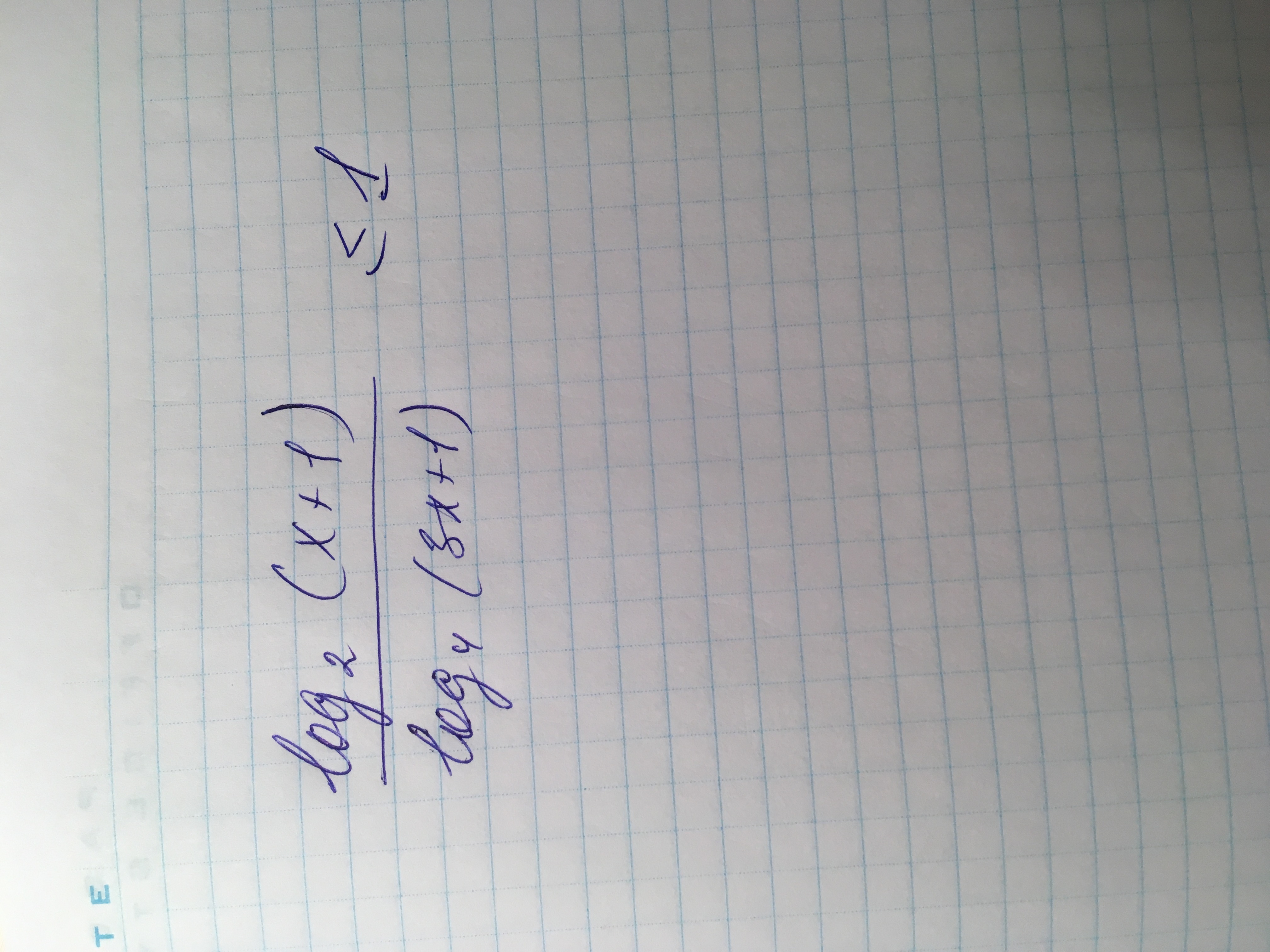
Ответы
Автор ответа:
1
Существует "модный" способ решения таких неравенств - метод рационализации. Но я предложу традиционный "старый" способ.

Рассуждаем далее: частное ≤ 0, когда числитель и знаменатель разных знаков, причем знаменатель ≠ 0. Рассмотрим 2 случая.
![1)\ \begin {cases} log_2(x+1)-log_4(3x+1) \leq 0 \\ log_4(3x+1)\ \textgreater \ 0 \end {cases}\\
\begin {cases} log_2(x+1)\leq log_4(3x+1) \\ log_4(3x+1)\ \textgreater \ 0 \end {cases}\ =\ \textgreater \
\begin {cases} x+1\ \textgreater \ 0 \\ 3x+1\ \textgreater \ 0 \\ 3x+1\ \textgreater \ 1\\ (x+1)^2\leq 3x+1 \end {cases}\\ =\ \textgreater \
\begin {cases} x\ \textgreater \ 0 \\ x^2+2x+1-3x-1 \leq 0 \end {cases} =\ \textgreater \ \begin {cases} x\ \textgreater \ 0 \\ x^2-x \leq 0 \end {cases} \\ =\ \textgreater \ \begin {cases} x\ \textgreater \ 0 \\ x(x-1) \leq 0 \end {cases} \ =\ \textgreater \ \boxed {x \in (0;1]} 1)\ \begin {cases} log_2(x+1)-log_4(3x+1) \leq 0 \\ log_4(3x+1)\ \textgreater \ 0 \end {cases}\\
\begin {cases} log_2(x+1)\leq log_4(3x+1) \\ log_4(3x+1)\ \textgreater \ 0 \end {cases}\ =\ \textgreater \
\begin {cases} x+1\ \textgreater \ 0 \\ 3x+1\ \textgreater \ 0 \\ 3x+1\ \textgreater \ 1\\ (x+1)^2\leq 3x+1 \end {cases}\\ =\ \textgreater \
\begin {cases} x\ \textgreater \ 0 \\ x^2+2x+1-3x-1 \leq 0 \end {cases} =\ \textgreater \ \begin {cases} x\ \textgreater \ 0 \\ x^2-x \leq 0 \end {cases} \\ =\ \textgreater \ \begin {cases} x\ \textgreater \ 0 \\ x(x-1) \leq 0 \end {cases} \ =\ \textgreater \ \boxed {x \in (0;1]}](https://tex.z-dn.net/?f=1%29%5C+%5Cbegin+%7Bcases%7D+log_2%28x%2B1%29-log_4%283x%2B1%29+%5Cleq+0+%5C%5C+log_4%283x%2B1%29%5C+%5Ctextgreater+%5C+0+%5Cend+%7Bcases%7D%5C%5C+%0A%5Cbegin+%7Bcases%7D+log_2%28x%2B1%29%5Cleq+log_4%283x%2B1%29++%5C%5C+log_4%283x%2B1%29%5C+%5Ctextgreater+%5C+0+%5Cend+%7Bcases%7D%5C+%3D%5C+%5Ctextgreater+%5C+%0A%5Cbegin+%7Bcases%7D+x%2B1%5C+%5Ctextgreater+%5C+0+%5C%5C+3x%2B1%5C+%5Ctextgreater+%5C+0+%5C%5C+3x%2B1%5C+%5Ctextgreater+%5C+1%5C%5C+%28x%2B1%29%5E2%5Cleq+3x%2B1++%5Cend+%7Bcases%7D%5C%5C+%3D%5C+%5Ctextgreater+%5C++%0A%5Cbegin+%7Bcases%7D+x%5C+%5Ctextgreater+%5C+0+%5C%5C+x%5E2%2B2x%2B1-3x-1+%5Cleq+0++%5Cend+%7Bcases%7D+%3D%5C+%5Ctextgreater+%5C++%5Cbegin+%7Bcases%7D+x%5C+%5Ctextgreater+%5C+0+%5C%5C+x%5E2-x+%5Cleq+0++%5Cend+%7Bcases%7D+%5C%5C+%3D%5C+%5Ctextgreater+%5C++%5Cbegin+%7Bcases%7D+x%5C+%5Ctextgreater+%5C+0+%5C%5C+x%28x-1%29+%5Cleq+0++%5Cend+%7Bcases%7D+%5C+%3D%5C+%5Ctextgreater+%5C++%5Cboxed+%7Bx+%5Cin+%280%3B1%5D%7D)

Наконец, объединяем ответы двух случаев:![\boxed {x \in (- \frac{1}{3}; 0) \cup (0;1]} \boxed {x \in (- \frac{1}{3}; 0) \cup (0;1]}](https://tex.z-dn.net/?f=%5Cboxed+%7Bx+%5Cin+%28-+%5Cfrac%7B1%7D%7B3%7D%3B+0%29+%5Ccup+%280%3B1%5D%7D)
Ответ:![(- \frac{1}{3}; 0) \cup (0;1] (- \frac{1}{3}; 0) \cup (0;1]](https://tex.z-dn.net/?f=%28-+%5Cfrac%7B1%7D%7B3%7D%3B+0%29+%5Ccup+%280%3B1%5D)
Рассуждаем далее: частное ≤ 0, когда числитель и знаменатель разных знаков, причем знаменатель ≠ 0. Рассмотрим 2 случая.
Наконец, объединяем ответы двух случаев:
Ответ:
BJIADA:
Спасибо!
Похожие вопросы
Предмет: Информатика,
автор: aaabbbxxxyyy17
Предмет: Право,
автор: tanya8892
Предмет: Русский язык,
автор: gffghczsfhb6hfd7
Предмет: Математика,
автор: SUBARU332