Предмет: Математика,
автор: dns937956
Решите плиззззз предел
СРОЧНООООО
Приложения:
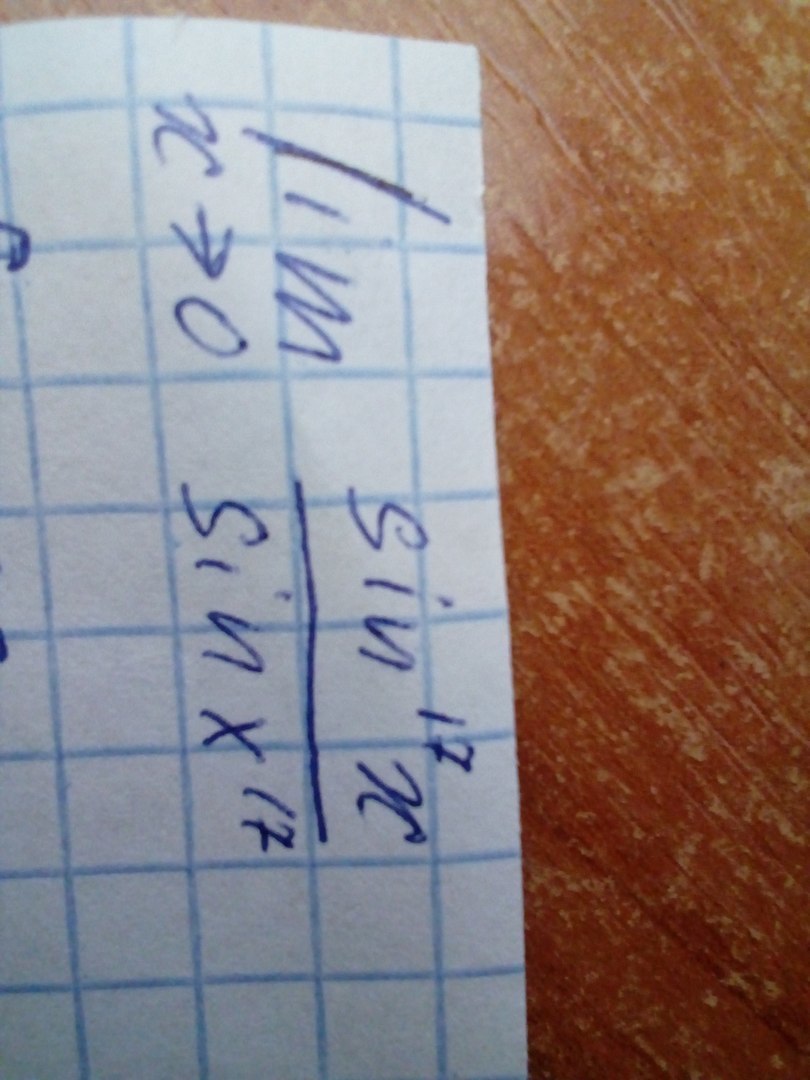
bearcab:
единица в ответе
да мне само решение нужно
можете плизз скинуть
Ответы
Автор ответа:
0
Раскладываем знаменатель в ряд по Маклорену по Пеано до третьего члена
Подставим в знаменатель
Ответ:1.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Українська мова,
автор: advukrain
Предмет: Русский язык,
автор: maksim22789
Предмет: Геометрия,
автор: voitex1
Предмет: Литература,
автор: незнайка597