Предмет: Геометрия,
автор: DanyaKotik
Найти площадь треугольника со сторонами 25, 25 и 14. Определите радиусы вписанной и описанной окружности.
Ответы
Автор ответа:
4
Дано:
ΔABC
AB = BC = 25
AC = 14
Найти:
R (описанной), r (вписанной) - ?
Решение:
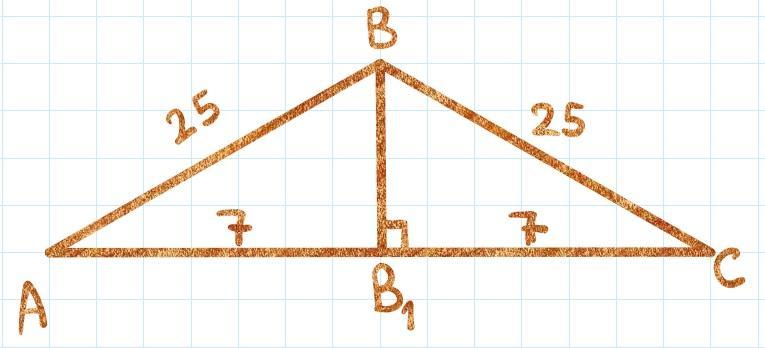
Для ΔABB₁ (∠B₁ = 90°) по теореме Пифагора:
AB² = AB₁² + BB₁²;
BB₁² = 25² - 7² = (25 - 7)(25 + 7) = 18 · 32 = 9 · 64 ⇒ BB₁ = 3 · 8 = 24;
SΔABC = ½ AC·BB₁ = 7 · 24 = 168;
p = ½P = ½ · (25 + 25 + 14) = 32 - полупериметр ΔABC;
r = S / p = 168 ÷ 32 = 5 1/4
R = (AB·BC·AC) / (4S) = (25 · 25 · 14) / (4 · 168) = 625/48 = 13 1/48
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: aboba242
Предмет: Литература,
автор: kitikflow
Предмет: История,
автор: chukmasova1966
Предмет: Математика,
автор: glina381
Предмет: Математика,
автор: kristina030612